DESCARGA EL PDF castellano DESCARREGA EL PDF català DESCARGA O PDF galego
Autor: Antonio J. Durán y Antonio Pérez Sanz
Aplicaciones interactivas: Daniel Ramos, José Antonio Mora, Débora Pereiro, Rafael Losada, José Luis Muñoz
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- Hardy y la belleza de las Matemáticas
- Toda Ley física debe tener belleza matemática
- Einstein, de descreído a venerador de las matemáticas
- Euler y el problema de Basilea. Elegancia e ingenio
- “Ver” las matemáticas. Belleza visual
- Potencias de números complejos
- Colores dinámicos
- Demostraciones visuales
- Op Art. Curvas de colores
- Débora. Esferas y zomes
- Bibliografía
Matemáticas (según el diccionario de la RAE): Ciencia deductiva que estudia las propiedades de los entes abstractos, como números, figuras geométricas o símbolos, y sus relaciones.

Aunque debería, no se incluye en esa definición un hecho fundamental: que, a menudo, es la emoción estética, el sentido de la belleza, la que guía al matemático cuando deduce o decide qué propiedades de los números o los entes abstractos va a estudiar. Los académicos de la lengua, más apegados a las cosas de las letras que a las de los números, no parecen haber advertido la inextricable ligazón entre matemáticas y belleza, de la que alguien dijo que era la verdadera guía en los grandes, y no tan grandes, descubrimientos matemáticos.
La belleza sitúa a las matemáticas a medio camino entre el arte y la ciencia: un arte con aplicaciones. Y esa importancia de los valores estéticos en las matemáticas refuerza la inevitable trabazón entre la ciencia abstracta por excelencia y la sensibilidad emocional propia de la especie humana.
«Puede ser sorprendente ver invocada la sensibilidad emocional a propósito de demostraciones matemáticas las cuales parecería que pueden interesar únicamente al intelecto. Esto sería olvidar el sentimiento de la belleza matemática, de la elegancia geométrica, que constituye un verdadero sentido de lo bello, conocido por todos los matemáticos y que con seguridad pertenece a la sensibilidad emocional».
Henri Poincaré
El hecho de que la belleza intrínseca de las matemáticas sea difícil de apreciar –porque no se percibe por un acto de percepción sensorial, como ocurre con la música o la pintura, sino por un proceso de pensamiento discursivo–, no la hace menos real.
La existencia de esa conexión entre belleza y matemáticas empezó a interiorizarse a raíz de los juicios de esos grandes creadores de opinión que fueron los filósofos clásicos griegos, especialmente Pitágoras, Platón y Aristóteles.
Para Platón, las cualidades de medida y proporción, esencia de la matemática griega, son sinónimo de belleza; mientras que, para Aristóteles, «Las formas que mejor expresan la belleza son el orden, la simetría, la precisión. Y las matemáticas son las que se ocupan de ellas especialmente».
Después han sido legión los científicos y pensadores que a lo largo de la historia han loado la belleza de las matemáticas. «La geometría es el arquetipo de la belleza del mundo», escribió Johannes Kepler en el siglo XVII; y, más recientemente, ya en el siglo XX, Bertrand Russell decía que: «Las matemáticas no solamente poseen la verdad, sino la suprema belleza, una belleza fría y austera, como la de la escultura, sin atractivo para la parte más débil de nuestra naturaleza».
Hardy y la belleza de las matemáticas
Quizá haya sido Godfrey H. Hardy quien mejor lo ha sabido explicar. Su magnífico A Mathematician’s Apology es, casi desde la primera hasta la última palabra, una defensa del valor estético de las matemáticas:

«La belleza es la primera piedra de toque; en el mundo no hay un lugar permanente para las matemáticas desagradables desde el punto de vista estético»
«Las configuraciones construidas por un matemático, lo mismo que sucede con las de un pintor o un poeta, deben poseer belleza; las ideas, los colores y las palabras deben ensamblarse de un modo armonioso»
Las auténticas matemáticas no repercuten de ningún modo sobre la guerra. Nadie ha podido descubrir ninguna finalidad bélica ni ninguna aplicación a la guerra que pueda derivarse de temas tales como la teoría de números o la relatividad, y parece bastante improbable que nadie pueda hacerlo en un futuro próximo
La insistencia de Hardy en la inutilidad de las «verdaderas» matemáticas ha sido considerada una muestra más de su faceta extravagante y provocadora. Porque es casi una provocación escribir:
Las auténticas matemáticas no repercuten de ningún modo sobre la guerra. Nadie ha podido descubrir ninguna finalidad bélica ni ninguna aplicación a la guerra que pueda derivarse de temas tales como la teoría de números o la relatividad, y parece bastante improbable que nadie pueda hacerlo en un futuro próximo.
Harold Hardy (1877-1947)
Casi a la vez que los Estados Unidos ponían en marcha el Proyecto Manhattan y fabricaban las primeras bombas atómicas. Hardy, a su manera, estaba declarando que en cuestiones de estética era un seguidor de Kant, o sea, defendía que las matemáticas son más arte –finalidad sin fin– que ciencia. Hardy describió las características que debían de tener las combinaciones de ideas matemáticas para generar valor estético:
|
generalidad y profundidad |
carácter inesperado y económico |
inevitabilidad |
A las que Gian Carlo Rota añadió también su capacidad iluminadora.
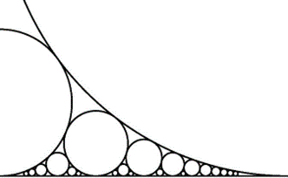
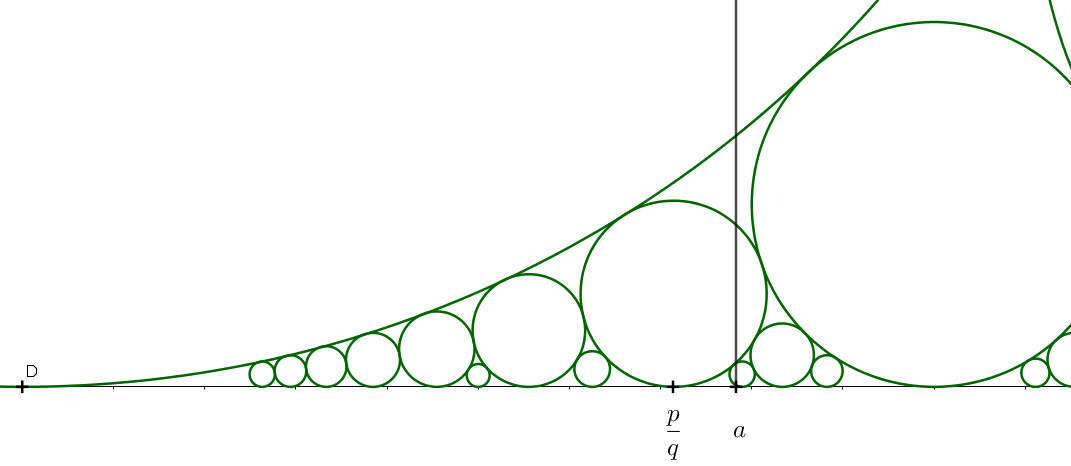
Todas estas características se dan en la combinación de ideas matemáticas que conecta tres resultados aparentemente tan dispersos como las circunferencias de Ford, el teorema de Hurwitz y la ecuación de Markov.


«Toda ley física debe tener belleza matemática»
La frase es de Paul Dirac, uno de los gigantes de la mecánica cuántica, premio Nobel de física en 1933.
El valor estético inherente a las matemáticas ha acabado fecundando también a la física, una ciencia más pegada a las cosas de este mundo que las matemáticas. Las cuestiones estéticas, incluidas las matemáticas, corresponden a la subjetividad humana y deberían ser una mala guía para explicar la naturaleza; sin embargo, según Dirac todo parece indicar lo contrario:
«El matemático juega un juego cuyas reglas ha inventado él mismo, mientras que el físico juega un juego en el que las reglas las determina la naturaleza; sin embargo, a medida que transcurre el tiempo, se hace cada vez más evidente que las reglas que el matemático ha encontrado interesantes son las mismas que la naturaleza ha elegido».

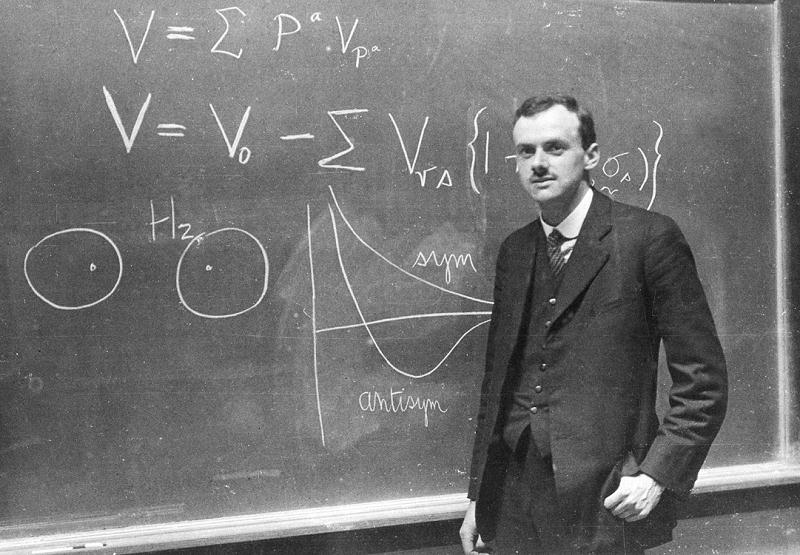
Einstein, de descreído a venerador de las matemáticas
El mismísimo Albert Einstein fue inicialmente un descreído de las matemáticas, de su simplicidad y belleza: «¡La belleza, señores, la dejaremos para los zapateros y para los sastres! El objeto de nuestra investigación ha de ser siempre la verdad», se le escuchó decir al inicio de su carrera como profesor. No mucho después, pasó a confiar en ellas como inspiración y guía de la indagación científica:
«Estoy convencido de que podemos descubrir, por medio de construcciones matemáticas puras, los conceptos y las leyes que los vinculan mutuamente y que nos proporcionan la clave para la comprensión de los fenómenos naturales. Por supuesto, la experiencia sigue siendo el único criterio de utilidad física de una construcción matemática. Pero el principio creativo reside en las matemáticas.
Creo que la naturaleza es la realización de las ideas matemáticas más simples concebibles».
Einstein acabó defendiendo que las leyes de la física eran una invención libre del espíritu humano, guiado por razones de estética y simplicidad matemática, que debían ser comprobadas por la observación; así lo expresó en varias ocasiones: «La ciencia no es simplemente una colección de leyes, un catálogo de hechos sin relación. La ciencia es la creación de la mente humana, con ideas y conceptos imaginados en libertad». En la última cita, Einstein entona para la física el grito de guerra de Georg Cantor: «La esencia de las matemáticas es la libertad».

Andrés Trapiello escribió: «La poesía es verdad indemostrable». La poesía pretende, según el diccionario de la RAE, manifestar la belleza o el sentimiento estético por medio de la palabra, en verso o en prosa. Las matemáticas, a fin de cuentas, son verdades demostradas, por lo que su universo no debe andar demasiado alejado del poético.
Euler y el problema de Basilea. Elegancia e ingenio
Grande será nuestra gratitud si alguien encuentra y nos comunica lo que hasta ahora ha escapado a nuestros esfuerzos.
Jakob Bernoulli
El mayor de los hermanos Bernoulli hablaba de la suma de una serie infinita que hasta la fecha había escapado a todos sus esfuerzos. La suma de los inversos de los cuadrados de los números naturales.
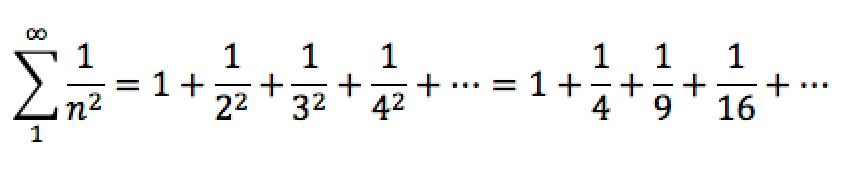
Planteada por primera vez por Pietro Mengoli en 1644, la serie atrajo la atención de los matemáticos más notables. Wallis calculó la suma con una aproximación de milésima: 1,645. Para ello tuvo que sumar más de 1000 términos de la serie. La serie converge pero muy lentamente.
Newton y Leibniz conocieron el problema. Y a través de este último llegó a los Bernouilli. Y fue Jakob quien desesperado lanzó el reto a los matemáticos europeos.
Christian Goldbach, en 1729, acotó la solución entre 41/35 y 5/3. Y James Stirling en 1730, dio hasta nueve cifras correctas de la suma: 1,644934066. Pero ¿qué era ese número?
 Y así llegó a las manos del genial Euler. En 1731 mejoró las aproximaciones a la suma. Euler calculó la suma de los mil primeros términos hasta encontrar un resultado con más de 20 decimales. Comprobó que se acercaba cada vez más a un número menor que 2:
Y así llegó a las manos del genial Euler. En 1731 mejoró las aproximaciones a la suma. Euler calculó la suma de los mil primeros términos hasta encontrar un resultado con más de 20 decimales. Comprobó que se acercaba cada vez más a un número menor que 2:
Pero ¿quién o qué era este número?, ¿cómo encontrar la solución del enigma?
Sus armas:
La genial demostración de Euler:
En 1735 ataca la demostración.
He encontrado ahora y contra todo pronóstico una expresión elegante para la suma de la serie que depende de la cuadratura del círculo… He encontrado que seis veces la suma de esta serie es igual al cuadrado de la longitud de la circunferencia cuyo diámetro es 1”.
Leonhard Euler
El problema de Basilea había sido resuelto.
La página 129 de su Introductio in Analysin Infinitorum es una de las páginas más hermosas de la historia de las matemáticas.

En ella aparecen las sumas de los inversos de las potencias pares de los números naturales. Desde los cuadrados a las potencias de exponente 20.
La suma de los inversos de las potencias impares sigue siendo un bello reto por resolver.
“Ver” las matemáticas. Belleza visual
La necesidad de “ver” las matemáticas no es en absoluto una moda de hoy en día. Matemáticos de todas las épocas han reivindicado la visualización de las ideas matemáticas:
- La palabra griega «θεωρηµα» (teorema) significa «lo que se contempla”.
- «La matemática es una ciencia del ojo” dijo Gauss
- «Es útil en muchas ocasiones describir estas figuras y mostrarlas a los sentidos externos para que de este modo se mantenga atento nuestro pensamiento más fácilmente». Descartes
Miguel de Guzmán en su libro El rincón de la pizarra afirma:
Las ideas, conceptos y métodos de las matemáticas presentan una gran riqueza de contenidos visuales, representables intuitivamente, geométricamente, cuya utilización resulta muy provechosa, tanto en las tareas de presentación y manejo de tales conceptos y métodos como en la manipulación con ellos para la resolución de los problemas de campo.
Las imágenes son parte fundamental del proceso matemático. Su utilización nos permite visualizar de forma rápida e intuitiva una idea, un enunciado matemático. Además, si esa imagen estática se puede convertir en dinámica conseguiremos generalizar un proceso con infinitos casos.
Tras esforzarnos por hacer ver a nuestros alumnos mediante construcciones visuales que deberían hacer absolutamente obvia una cierta situación matemática, algunos nos piden: “Ahora, por favor, una verdadera demostración matemática”.
¿Qué es una demostración? Para los pitagóricos, que jugaban con piedras, probablemente sería: “¡contempla!”
En la actualidad los programas de geometría dinámica hacen posible visualizar esos conceptos, ideas y resultados matemáticos y lo hacen incluso de una forma estética y agradable a nuestros sentidos.
Aquí hay una selección de esas matemáticas visuales, plenas de otra forma de belleza matemática:
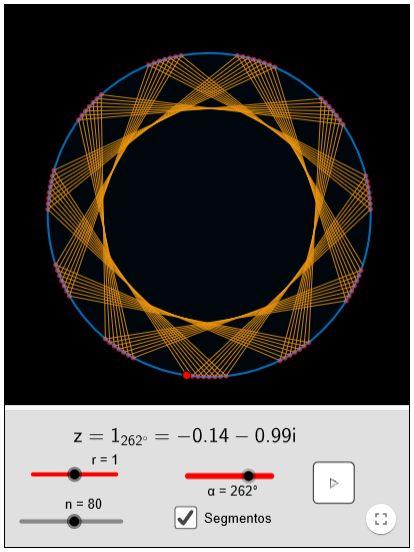
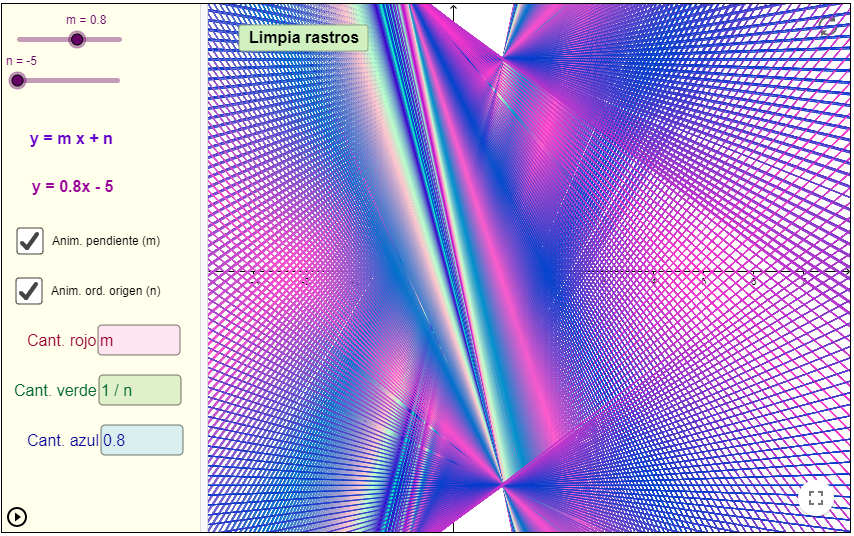
Potencias de números complejos
Las matemáticas nos descubren el atractivo estético de sus estructuras y de sus regularidades en los lugares más insospechados. Sólo hay que saber mirar y contar con los lentes adecuados.
Si observamos las sucesivas potencias de números complejos con módulo 1 o próximo a 1 descubriremos la magia de la simetría en acción.
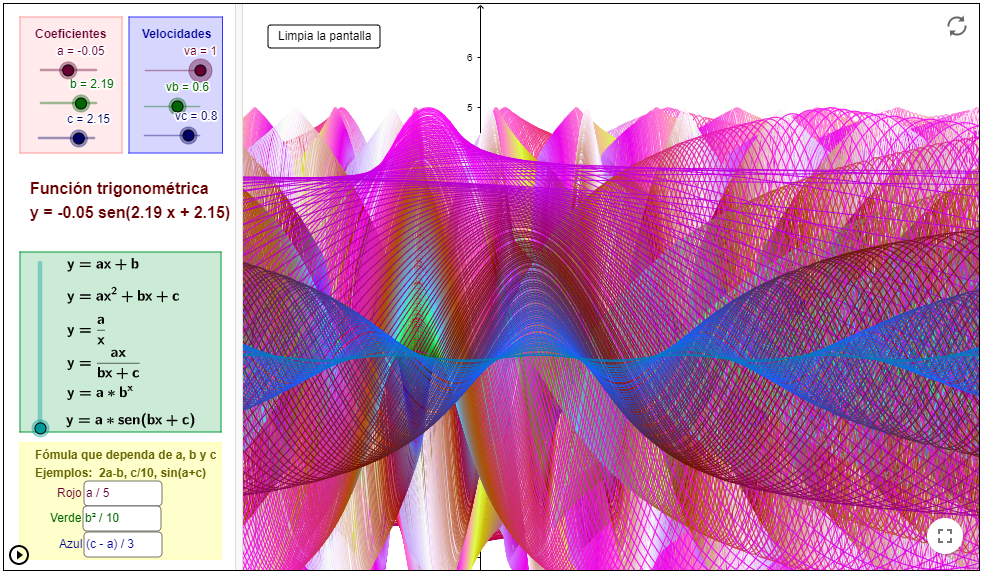
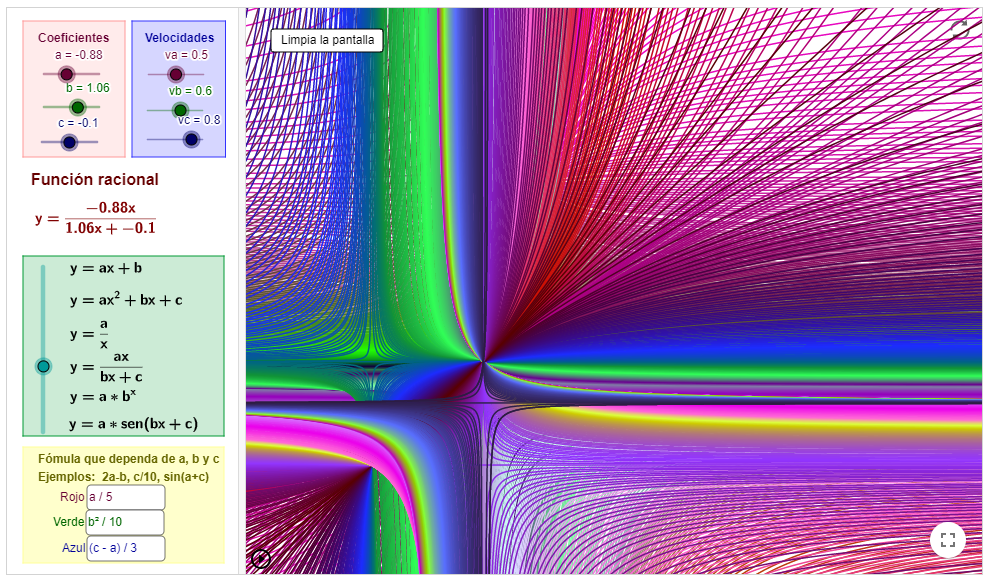
Colores dinámicos
Más adelante descubro que la propiedad Color Dinámico que poseen los objetos creados con GeoGebra permite visualizar fácilmente puntos o lugares geométricos desconocidos, sin necesidad de construir ni un punto del lugar, siempre que sepamos expresar la condición que deben cumplir los puntos del mismo.
Rafael Losada
Efectivamente, el desarrollo actual del software de matemáticas nos permite ver esos fantasmas geométricos, eso sí, hay que saber invocarlos correctamente. El funcionamiento recuerda a una radiografía o una tomografía del objeto geométrico.
Este escáner permite el mapeado del plano descubriendo aquellos lugares donde se cumple una determinada relación o propiedad, incluso desconociendo la forma de construir tal lugar geométrico. Y los resultados, además de prácticos son un placer para la vista.
Demostraciones visuales
Op Art. Curvas de colores
El término op art (arte óptico) fue acuñado por Time Magazine en 1964. El Op art explora los efectos ópticos que pueden obtenerse del uso de formas geométricas y contrastes de color. Geogebra dispone de varias herramientas para modificar el color de los objetos que construimos y nos permite experimentar efectos plásticos con gráficas de las funciones elementales.
Débora. Esferas y zomes
Desde que Platón en su diálogo Timeo asignase a la esfera el papel de forma perfecta, las esferas solas o en racimo han ejercido un cautivador atractivo entre matemáticos, astrónomos, geógrafos y artistas.
Escher no pudo sustraerse al embrujo de las esferas y nos dejó geniales interpretaciones de la representación de curvas espirales sobre una superficie esférica y hasta su propio autorretrato reflejado en una esfera.



Geogebra nos permite hoy jugar a ser Escher y hacer representaciones artísticas de gran plasticidad sobre esferas y otras superficies curvas. Dëbora Pereiro nos ofrecen un amplio muestrario de ideas en su libro Esferas y zomes
Y como despedida nada mejor que la belleza del despertar de una flor.
Bibliografía
CARVAJAL SÁNCHEZ, A. MUÑOZ CASADO, J.L. Demostraciones visuales en matemáticas. Ed. La Catarata. Madrid 2020
DUNHAM, W. Euler. El maestro de todos los matemáticos. Ed. Nivola. Madrid 2006
DURÁN, A. J. La poesía de los números. El rol de la belleza en matemáticas. Ed. RBA. 2010.
GUZMÁN, M. de. El rincón de la pizarra. Ed. Pirámide. Madrid 1997.
GUZMÁN, M. de. Mirar y ver. Ed. Nivola. Madrid 2002
HARDY, G.H. Apología de un matemático. Ed. Nivola. Madrid 1999
NELSEN, R. Demostraciones sin palabras. Proyecto Sur Ediciones. Granada 2001
STEWART, I. Belleza y verdad. Ed. Crítica. Barcelona. 2008