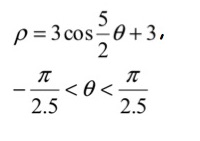DESCARGA EL PDF castellano  DESCARREGA EL PDF català  DESCARGA O PDF galego

Autor: Daniel Ramos y Antonio Pérez 
Aplicaciones interactivas:  José Manuel Arranz, José Luis Muñoz y  Débora Pereiro
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)

CONTENIDO

Los antiguos griegos basaron toda su geometría en las construcciones que se pueden hacer con regla y compás: la recta y la circunferencia. Son las líneas más simples, y encarnan el concepto de distancia: un segmento de línea recta realiza la distancia entre dos puntos; un compás permite trasladar distancias de un sitio a otro, y por tanto son las herramientas ideales para hacer geometría. Sin embargo, hay muchas otras curvas que aparecen en geometría, como las secciones cónicas (elipses, parábolas, hipérbolas), y muchas otras más complejas.

Curvas para resolver problemas

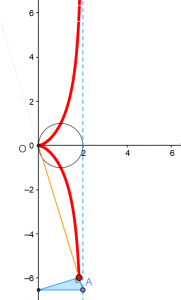
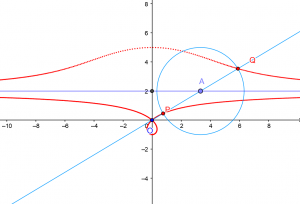
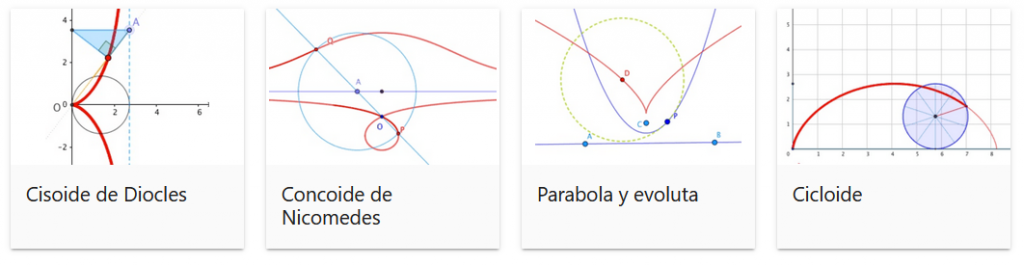
La Cisoide de Diocles o la Concoide de Nicomedes son curvas definidas mecánicamente, que los griegos usaron para resolver problemas clásicos como la duplicación del cubo (dado un cubo, hallar el lado de otro con volumen doble) o la trisección del ángulo (dividir un ángulo cualquiera en tres partes iguales), pues no hallaban construcciones más simples. No fue hasta en el siglo XIX cuando se demostró que es imposible resolver esos problemas con regla y compás.

Cisoide de Diocles
Concoide de Nicomedes

 

Midiendo la curvatura

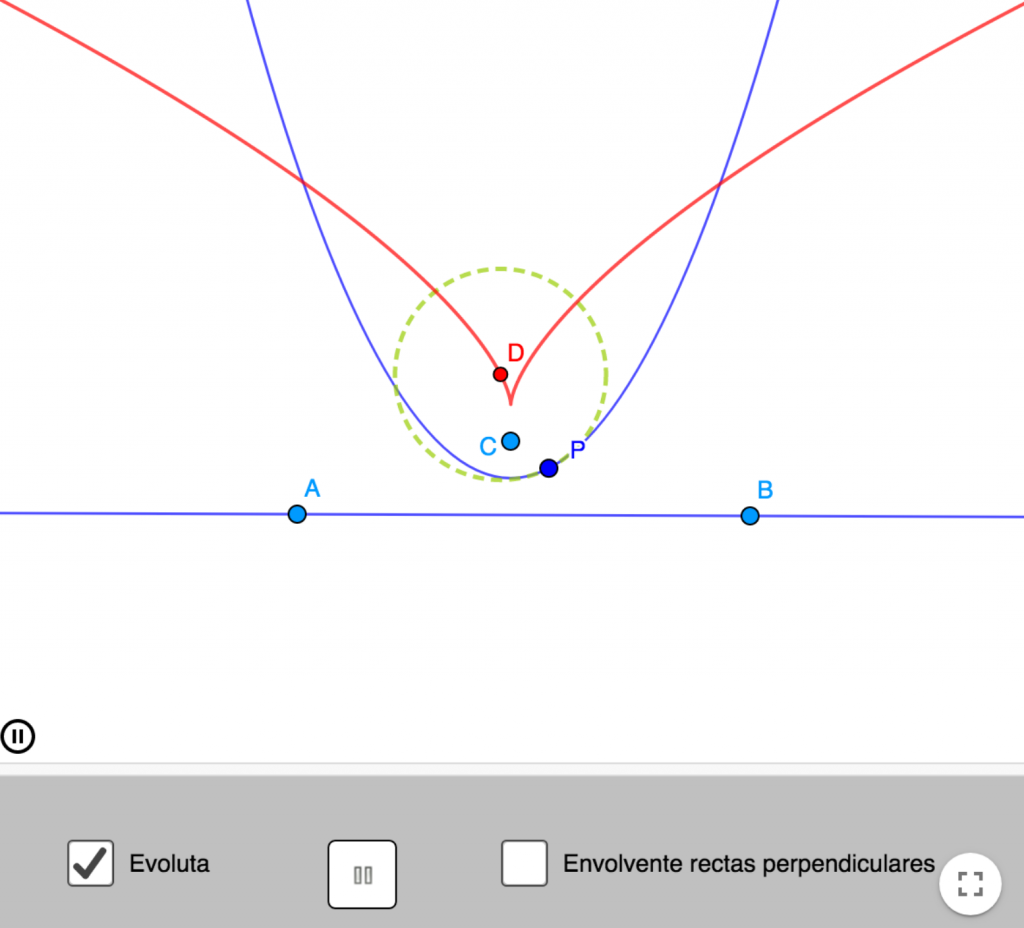
Evoluta de una parábola

Podemos medir cuán curvada está una línea. Intuitivamente, una recta no lo está, y la curvatura de una circunferencia se mide por su radio (cuanto menor es el radio, mayor es su curvatura). Con una curva cualquiera, la podemos aproximar en primer orden por una recta tangente (que pasa por dos puntos infinitesimalmente cercanos), y en segundo orden por la circunferencia osculatriz (que pasa por tres puntos infinitesimalmente cercanos). Así, en ese punto, la recta tangente nos da la dirección, y la circunferencia osculatriz su curvatura. Su centro y radio se denominan centro de curvatura y radio de curvatura respectivamente. El conjunto de todos los centros de curvatura se denomina la evoluta de la curva original.

Puedes ver todas estas curvas en esta aplicación:

Al diseñar el trazado de una carretera o las vías de un tren, los ingenieros deben calcular el radio de curvatura mínimo de la curva en cada punto, que dependerá de la velocidad a la que los coches o trenes vayan a circular.

¿Son siempre paralelas las ruedas delanteras de un coche? No, para que el coche tome la curva suavemente, los ejes de las ruedas deben apuntar hacia el centro de curvatura de la carretera, además de girar 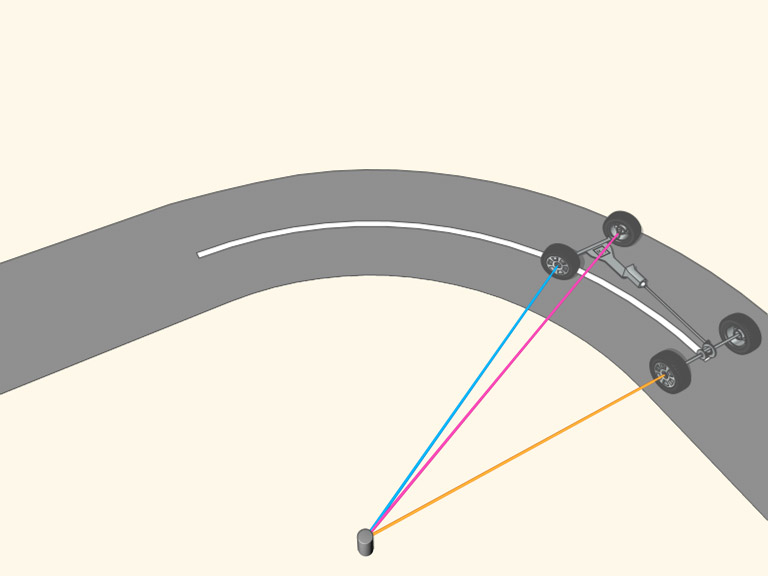a velocidades diferentes. ¿Y en un tren? En este caso las ruedas sí que son paralelas, pero las ruedas tienen la forma de una superficie cónica, de manera que al tomar una curva, el tren se inclina ligeramente y el radio efectivo de la rueda (del eje al punto de contacto) es diferente para la rueda del lado interior y exterior.

En una recta o una curva podemos movernos hacia adelante o hacia atrás. Si añadimos otra dimensión, para movernos a izquierda o derecha, nos movemos en una superficie. El plano es la superficie más simple pero hay muchas superficies posibles.

Enrollando y desenrollando

Los radios de curvatura de una curva son segmentos tangentes a la evoluta. Esto sugiere que para recuperar la curva original a partir de su evoluta, se puede imaginar que despegamos un hilo que se encuentra adherido a la curva evoluta.

Este procedimiento se denomina hallar la involuta de una curva. La involuta de la evoluta (o en orden inverso) es esencialmente la curva de partida.

La curva que es evoluta e involuta de sí misma es la cicloide. Es la curva que describe un punto de una rueda que gira sin deslizar sobre una recta. Entre sus muchas propiedades, dispuesta con sus puntas hacia arriba es la curva por la que un objeto desciende más rápido por acción de la gravedad, y además lo hace en un tiempo independiente de la altura inicial.

Esto servía por ejemplo para péndulos de relojes de precisión, donde el período del péndulo es constante independientemente de la amplitud de la oscilación

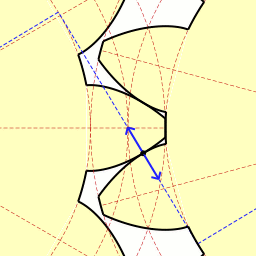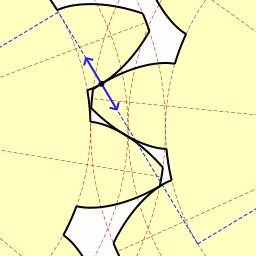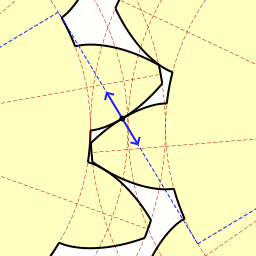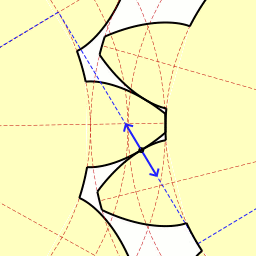La involuta de una circunferencia aparece en las ruedas dentadas de precisión. Las tangentes en el punto de contacto de los dos dientes coinciden.

Esta forma de los dientes de los engranajes garantiza una transferencia suave de la fuerza en cada momento, y una proporción constante entre las velocidades angulares de ambas ruedas. Además las superficies de desgaste activo se distribuyen de manera más uniforme y las vibraciones son más bajas que con cualquier otro perfil.

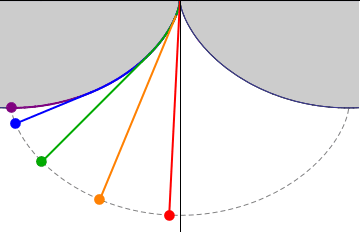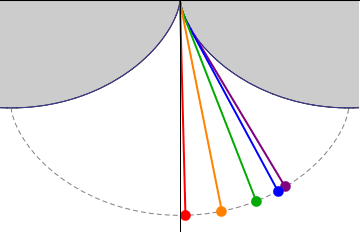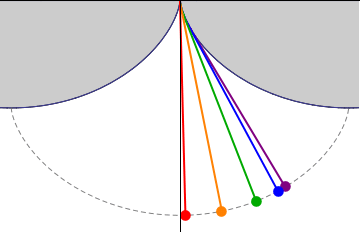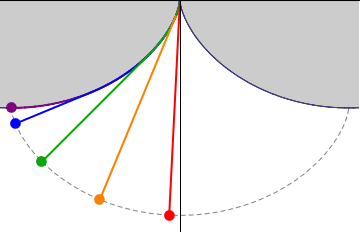
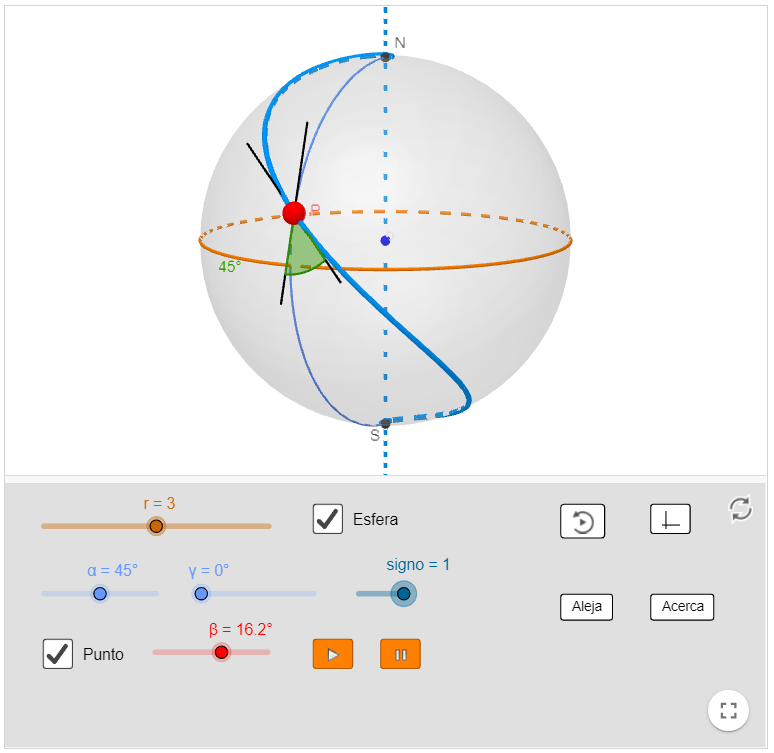
Vivimos sobre una enorme esfera casi perfecta, nuestro planeta Tierra. Si queremos navegar una gran distancia a través del océano, querremos hacerlo por la ruta más corta, que no puede ser una línea recta ya que no podemos abandonar la superficie curvada del planeta. La curva más corta entre dos puntos se denomina geodésica, y en el caso de una esfera, son arcos de circunferencias máximas con el mismo centro que la esfera.

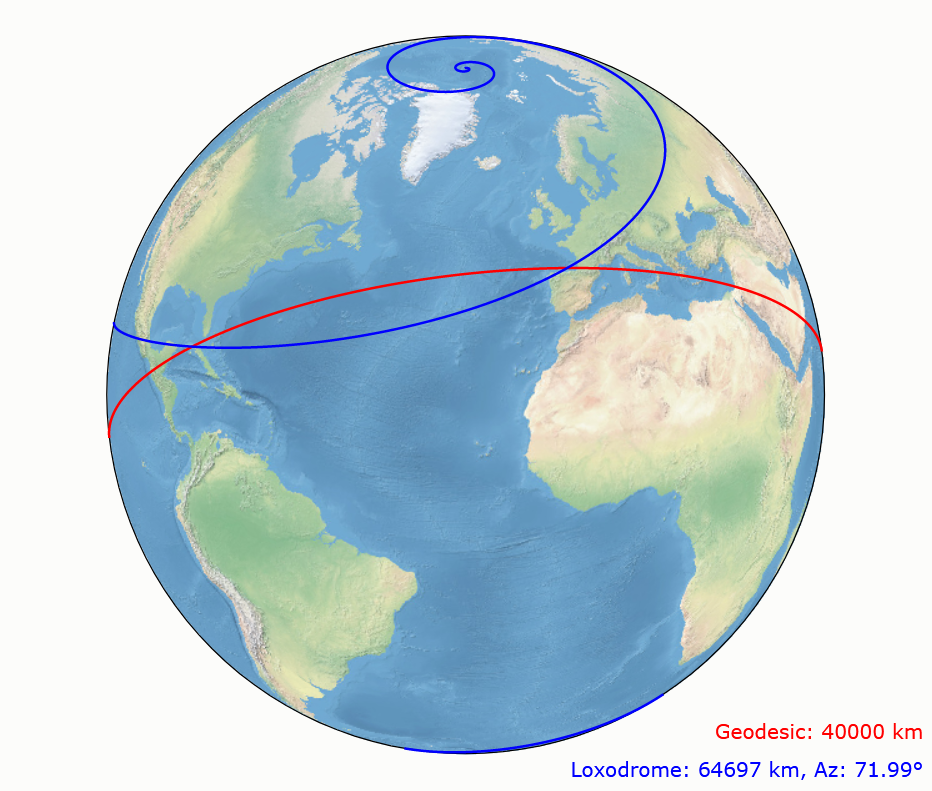
Dos rutas entre la Habana y Vigo. En rojo la más corta (geodésica, 6900 km), en azul la más fácil (loxodroma, 7050 km), que guarda un ángulo constante de 72º con la dirección del Norte.

Para navegar la Tierra, sin embargo, la línea más fácil de seguir es la que forma un ángulo constante con el Norte, que podemos conocer con una brújula o las estrellas

Esta curva, llamada loxodroma, fue la base de las exploraciones marítimas desde el siglo XVI. No existe ningún mapa que represente la Tierra a escala, debido a la curvatura de la esfera (lo demostró Gauss en 1827), pero el mapa de Mercator (creado por Gerardus Mercator en 1569) representa las loxodromas por líneas rectas y permite así hallar líneas de rumbo.

Superficies singulares

Otras superficies más complejas se pueden definir mediante procedimientos mecánicos o algebraicos, al igual que con las curvas.

Una ecuación que involucre las variables x, y, z define una superficie formada por todos los puntos del espacio cuyas coordenadas satisfacen esa ecuación.

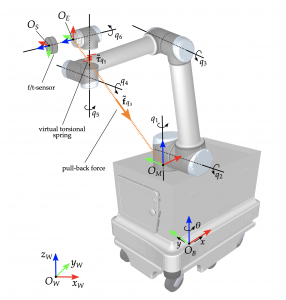
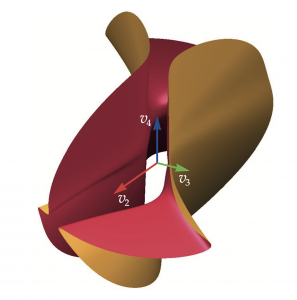
Un brazo robótico con diferentes articulaciones (variables de grados de libertad). Las relaciones entre esas variables forman una ecuación algebraica. En la imagen, representación de sus singularidades (por ejemplo, cuando el brazo está extendido y rotar una articulación pierde su efecto)

M. Weyrer, M. Brandstötter and M. Husty

A veces, estas superficies tienen puntos singulares, donde la superficie no es lisa, que tienen especial interés en matemáticas y en sus aplicaciones.

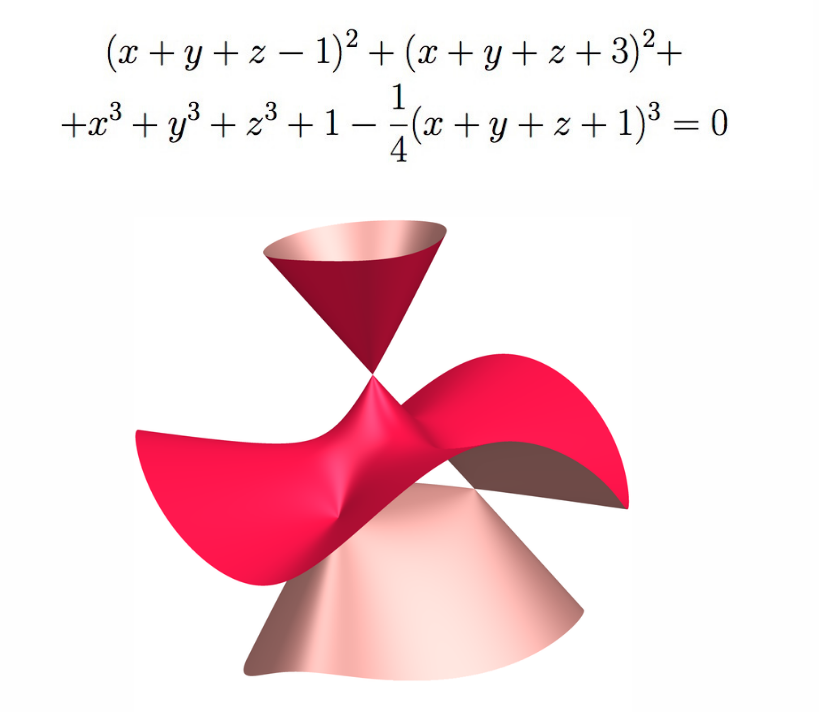
Una superficie algebraica, con su ecuación.Es una cúbica (grado 3) con cuatro puntos singulares

El espacio y el universo

Una curva puede estar contenida en un plano, en una superficie o, en general, en el espacio tridimensional. Esto es lo que sucede por ejemplo con las trayectorias de cohetes y sondas espaciales, que están definidas por sus motores y sobre todo por las fuerzas gravitatorias de la Tierra y otros objetos celestes. De hecho la teoría de la Relatividad General de Einstein nos dice que en realidad la gravitación es una deformación del espacio-tiempo, así que las trayectorias de objetos libres son geodésicas un espacio curvo, e incluso la luz sigue estas trayectorias curvadas.

NASA-STSCI. Ecuación de Einstein para la Relatividad General.A la izquierda del signo igual, los tensores que miden la geometría;a la derecha, los que miden la energía-materia y sus propiedades físicas.La igualdad significa que la energía-materia deforma y curva el espacio.
NASA/GoddardTrayectoria orbital de la sonda ARTEMIS-P1 alrededor de la Luna.Los puntos de Lagrange L1 y L2 son aquellos donde las fuerzas de atracción gravitatoria y/o centrífuga de la Tierra y la Luna se cancelan.
Interstellar-©-Warner-Bros

Event Horizon Telescope Collaboration

NASA

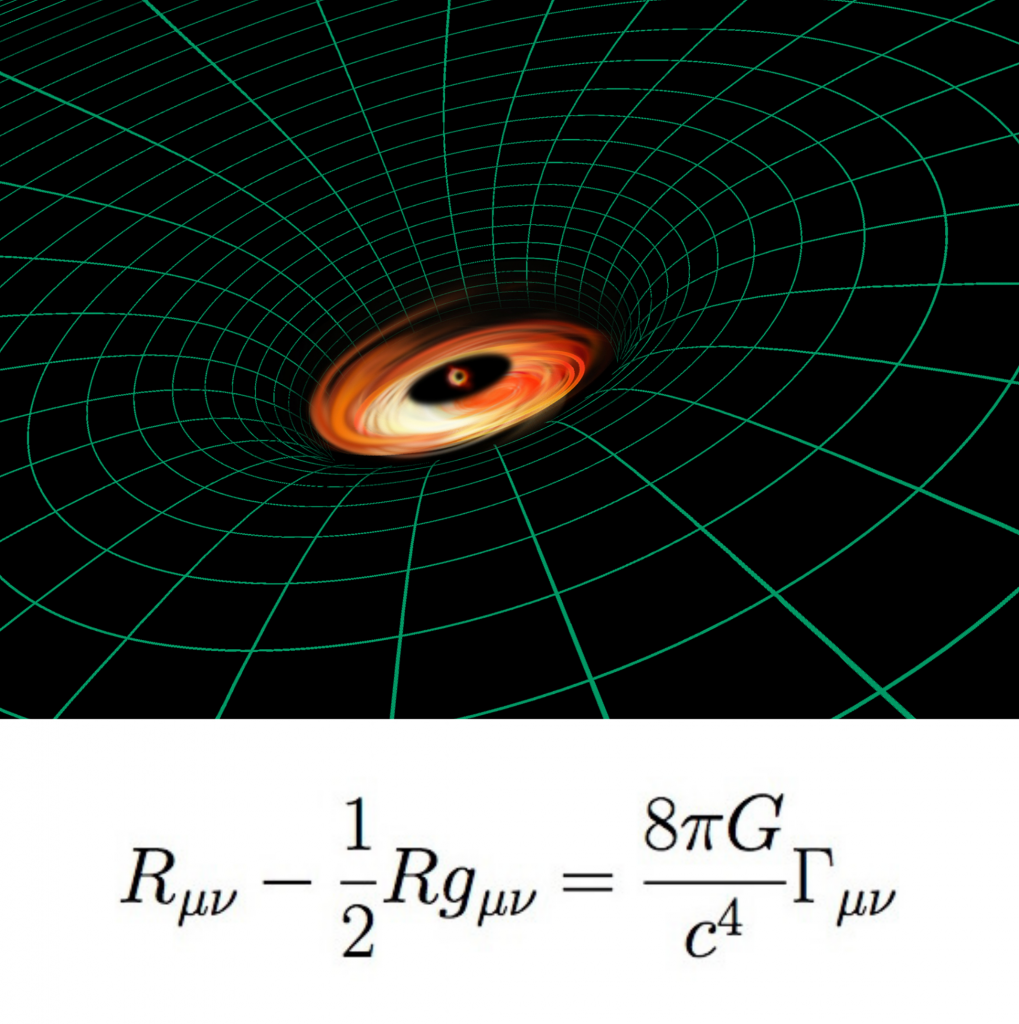
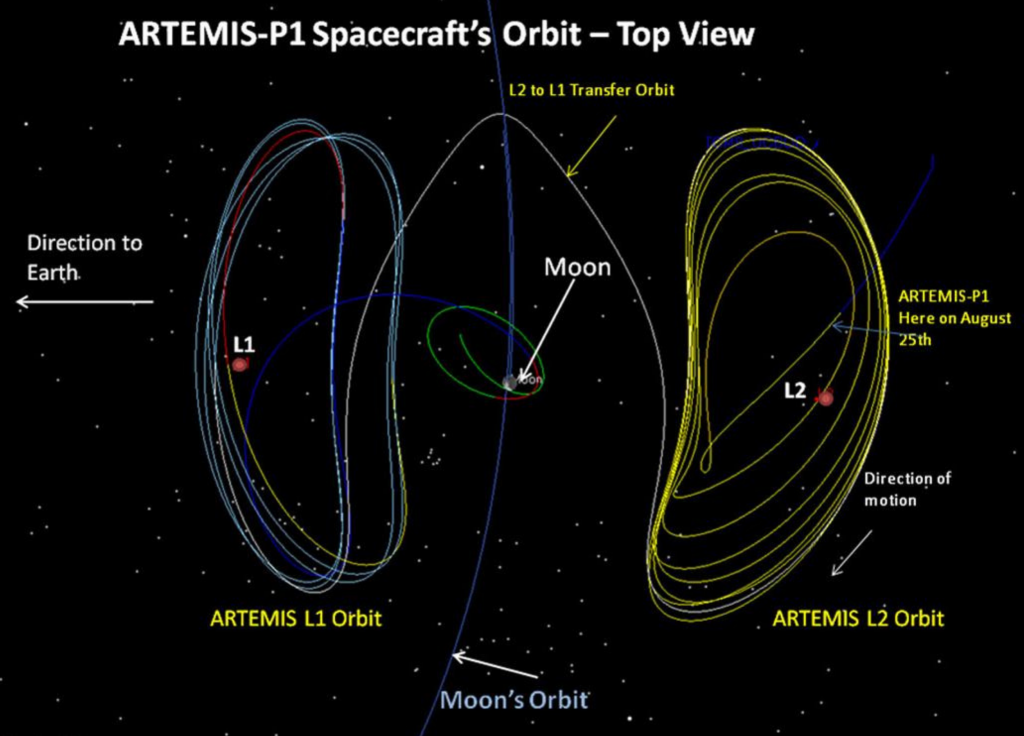
Simulaciones de un agujero negro que tuviese un disco de acreción alrededor, formado por materia radiante que girase a su alrededor. El agujero en sí no emite luz (es negro), la luz no puede escapar de él. La luz emitida por el disco se curva alrededor del agujero, y es percibida por un observador como un halo alrededor de un círculo negro.

En el centro de las tres imágenes anteriores puedes observar la primera imagen real de un agujero negro, tomada en 2019 por el Event Horizon Telescope.

El universo de las curvas. De los planetas a las flores

A lo largo de la historia las curvas han sido el instrumento ideal para explicar fenómenos y formas de la Naturaleza.

Los planetas: de los epiciclos a las cónicas

Los antiguos griegos ya habían observado que los planetas conocidos describían órbitas erráticas sobre el fondo de estrellas fijas. De hecho el término planeta significa “errático” o viajero. A veces, incluso parecen retroceder en sus órbitas.

Aristóteles, defensor de que en el cielo todo movimiento se ajusta a las formas perfectas de la esfera y el círculo, recurre a un modelo físico basado en esferas de éter en las que se mueven los planetas. Estas esferas se van acelerando y frenando unas con otras. El complejo mecanismo necesitaría de 56 esferas distintas para poder explicar los movimientos aparentes de los planetas. Este modelo condenó a los astrónomos a moverse sólo en círculos durante muchos siglos.

Epiciclos y deferentes

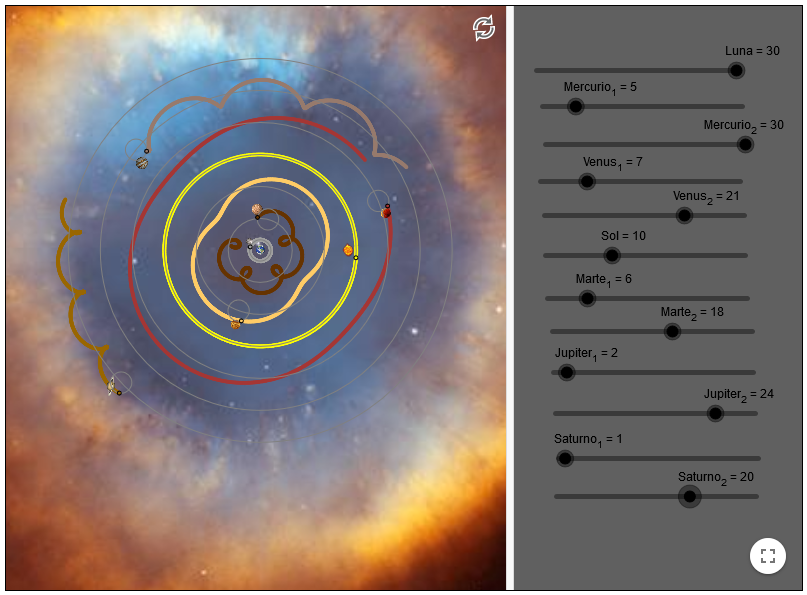
Para explicar el movimiento de los planetas respetando la idea de que sólo se pueden mover en órbitas circulares Ptolomeo va a inventar un ingenioso modelo geométrico: los epiciclos y los deferentes.

A cada planeta, incluidos el Sol y la Luna, les asigna un círculo imaginario llamado deferente. La Tierra está en interior de este círculo, aunque no necesariamente en el centro. El planeta girará en un nuevo círculo llamado epiciclo cuyo centro será un punto del círculo deferente.

Al moverse el centro del epiciclo a lo largo de la deferente, al planeta se acerca o se aleja de la Tierra lo que explicaba a la perfección los cambios de brillo de un mismo planeta observados en distintos momentos del año.

La idea de hacer rodar círculos sobre círculos nos abre las puertas a un sugerente mundo de curvas mecánicas generadas mediante el movimiento uniforme y que nos introduce en un paraíso de curvas. Astroides, cardiodes… y hasta elipses. Sí, aunque parezca increíble los epiciclos y deferentes de Ptolomeo pueden generar órbitas elípticas.

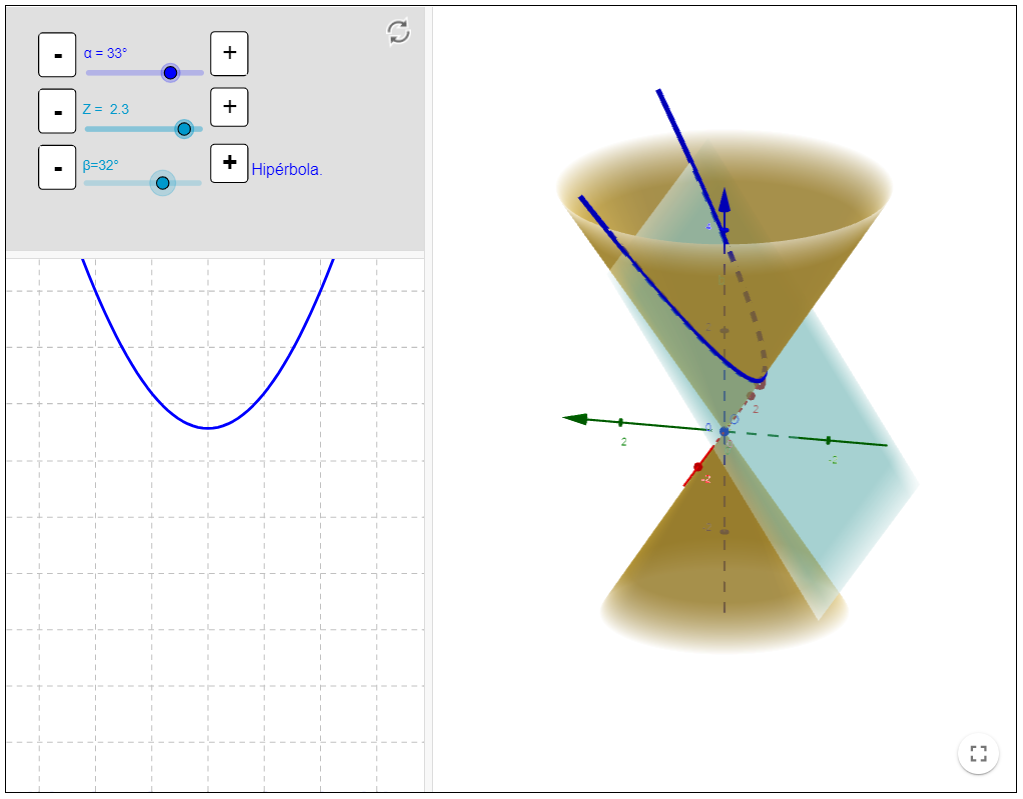
Las cónicas: de Apolonio a Kepler

Las cónicas están muy cerca de nosotros. Cada vez que bebemos en un vaso nos acercamos a los ojos al menos dos de ellas: un círculo y una elipse. Y si miramos las sombras proyectadas en una pared por una de esas lámparas que tenemos en nuestro salón es fácil encontrar las cuatro cónicas. Sólo hace falta inclinarla de forma conveniente.

En su origen en la Grecia clásica las cónicas de Menecmo y Apolonio sirvieron como herramientas para resolver dos problemas clásicos: la duplicación del cubo y la trisección de un ángulo. Pero alcanzarán la gloria en el Renacimiento de la mano de Kepler.

Con la primera de sus famosas leyes destierra a la circunferencia aristotélica y la sustituye por la elipse:

Primera Ley Los planetas describen órbitas elípticas en uno de cuyos focos está el Sol.

Y tras Kepler, Newton descubrirá que todos los objetos de nuestro sistema solar se mueven con trayectorias que describen una de las cónicas.

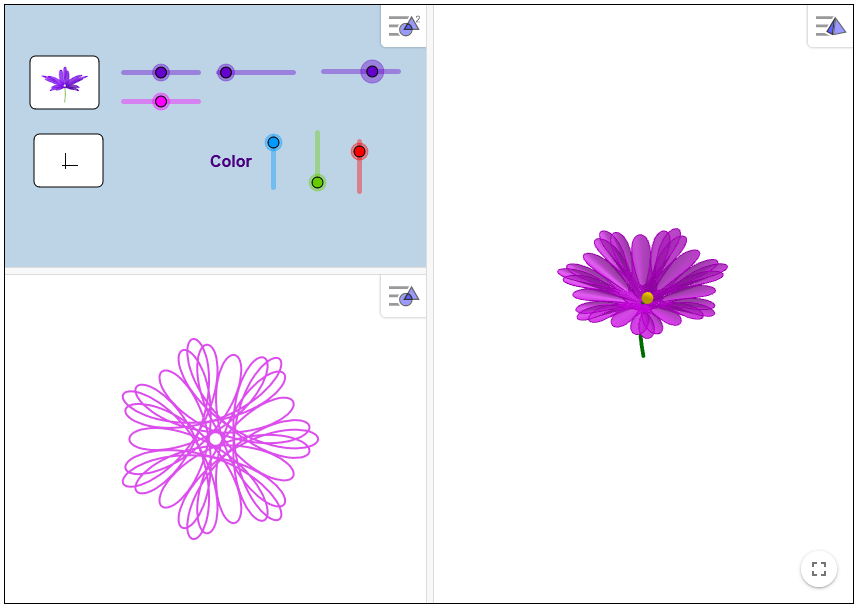
Y todo nació al cortar con un plano la superficie de un cono…

Las flores. Las curvas botánicas

En apariencia las hojas de las plantas y los pétalos de las flores están hermanados con la poesía y muy alejados de las matemáticas. Sin embargo también podemos acercarnos a los misterios del crecimiento vegetal a través de curvas y de ecuaciones, y además no demasiado complejas.

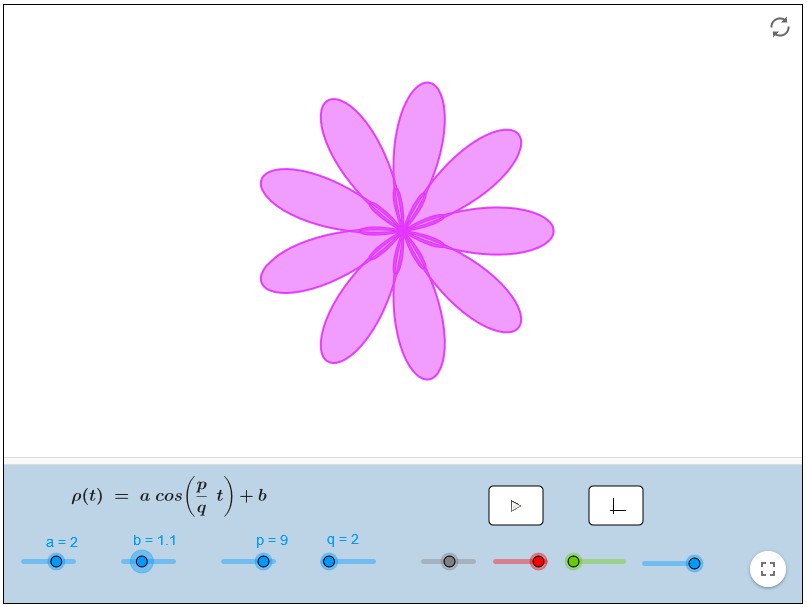
Existe una familia de curvas, investigada en el siglo XVIII, que parece haber nacido para identificarse con algunas de las flores que podrás encontrar esta primavera en el Jardín botánico y en tus excursiones por el campo.

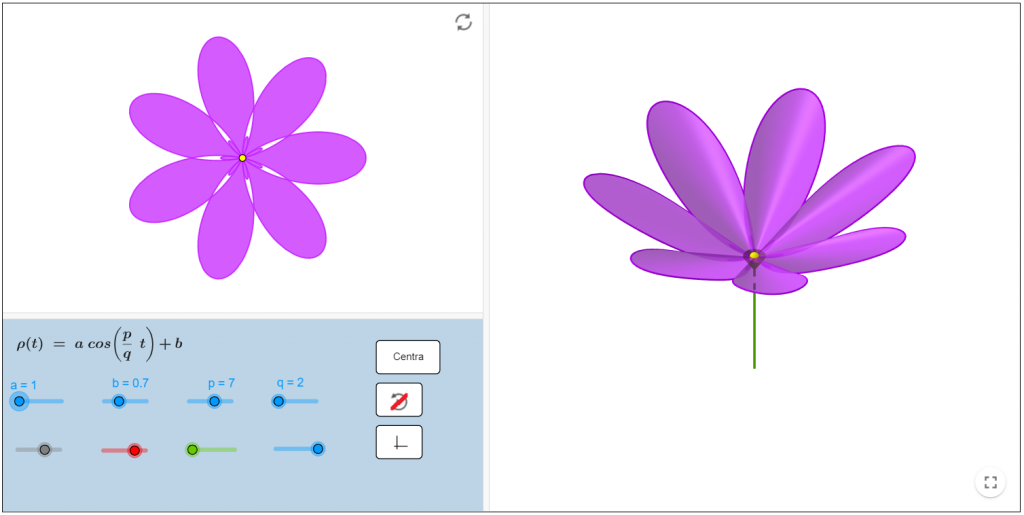
Se trata de la concoide de rosetón, también conocida como pétalo geométrico. Para interpretar el crecimiento de hojas y flores las coordenadas rectangulares o cartesianas no son las más apropiadas. Recurriremos a las coordenadas polares, en las que las dos variables son el ángulo girado respecto a la horizontal y la distancia al origen. Su ecuación es

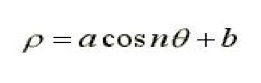
Puedes comprobarlo y practicar con este applet:

Cada pétalo base es simétrico respecto del eje OX y se obtiene haciendo variar el ángulo  entre

Haciendo variar los valores de a, b y n podemos obtener casi todas las siluetas de los pétalos de las flores.

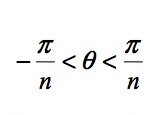
Superficies. Encuentros en el espacio entre Geometría y Álgebra

Superficies de revolución

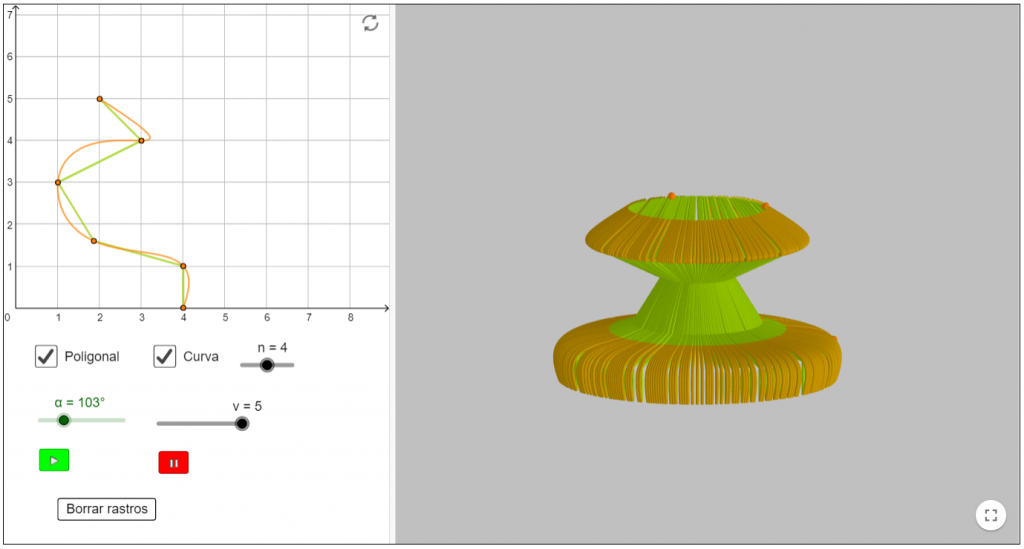
Las superficies del alfarero. Si haces girar una curva alrededor de un eje obtienes una superficie de revolución. Es lo que hacen magistralmente los alfareros con el torno.

Superficies regladas

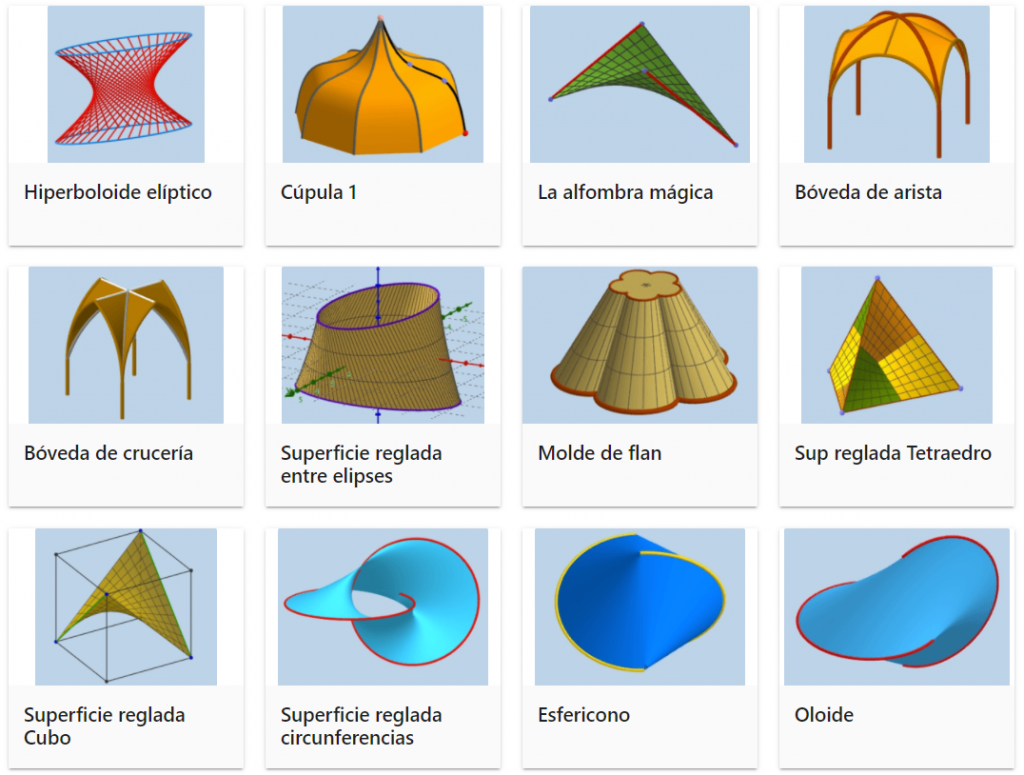
Las superficies regladas son las que se pueden generar mediante el movimiento de una recta o un segmento de recta al desplazarse sobre una o varias curvas.

Muchos arquitectos trabajan con superficies regladas. Añaden a la belleza de sus formas las ventajas de su construcción: permiten el uso del hormigón de forma sencilla y proporcionan rigidez a la estructura.

En esta aplicación de José Manuel Arranz puedes encontrar un amplio catálogo de superficies regladas.

Superficies algebraicas

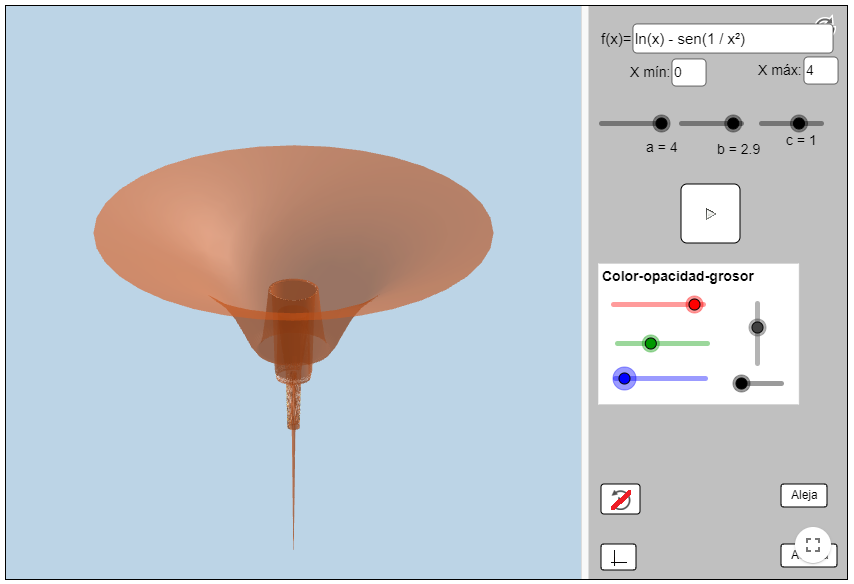
Una simple ecuación puede determinar una forma en el espacio. Una forma delimitada por una o varias superficies, con sus curvas, sus agujeros, sus pliegues.

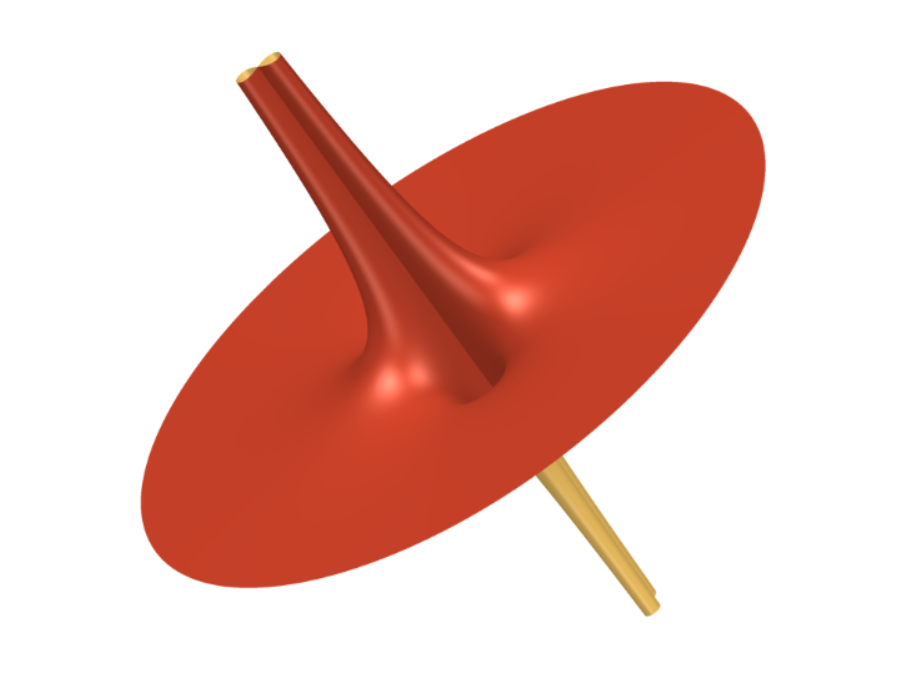
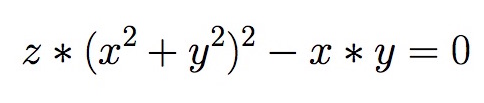
Las superficies algebraicas vienen determinadas por una simple ecuación en la que juegan las variables x, y, z , y las operaciones que conoces desde pequeño, suma, resta, multiplicación… Las ternas (x,y,z) son las coordenadas de los puntos del espacio. Los puntos que verifican la ecuación forman la superficie.

Los picos, pliegues o aristas en las superficies son singularidades. Pequeños cambios en la ecuación cerca de esos puntos pueden cambiar su aspecto de forma increíble.

En la web de Imaginary puedes descargar un excelente programa para representar superficies algebraicas.

Ecuaciones en forma explícita, implícita o paramétricas nos permiten sumergirnos en un mundo mágico de las superficies. Las ecuaciones esconden más belleza de la que te podías imaginar.

Flores en 3D

Al igual que las flores secas aprisionadas entre las páginas de un libro pierden parte de su encanto, las ecuaciones en el plano de las flores tienen algo de flor seca.

Si queremos aproximarnos a la auténtica belleza matemática de las flores tendremos que verlas en 3D.

Débora Pereiro nos aproxima en estos dos applets a ese mundo mágico de las flores vistas con ojos matemáticos y nos permite jugar a experimentar como auténticos botánicos en la creación de nuestras propias flores.

Aquí podrás construir tus propias flores. Y si tienes paciencia hasta verás volar mariposas a su alrededor.

Y aquí encontrarás un auténtico jardín botánico-matemático.

Bibliografía

ÁLVAREZ PÉREZ J.M. Curvas en la historia. Ed. Nivola.2006

D´ARCY THOMPSON. Sobre el Crecimiento y la Forma. Blume Ediciones. Madrid 1980

COURANT Y ROBBINS. ¿Qué son las Matemáticas? Fondo de Cultura Económica. México.2002

DORCE, C. Ptolomeo. El astrónomo de los círculos. Ed. Nivola. Madrid 2005

GHYKA M. Estética de las proporciones en la Naturaleza y en las Artes. Poseidon. Barcelona. 1983.

HILDEBRANDT Y TROMBA. Matemáticas y Formas Óptimas. Prensa científica. Barcelona. 1990

PÉREZ SANZ, A. Las ecuaciones de las flores. Sigma: revista de matemáticas = matematika aldizkaria, ISSN 1131-7787, Nº. 26, 2005, págs. 137-148

RÍO SÁNCHEZ, J. del. Lugares geométricos. Cónicas. Ed. Síntesis. Madrid 1991

RSME. Imaginary. Una mirada matemática. www.rsme_imaginary.es. Gijón. 2010

Créditos de las imágenes