DESCARGA EL PDF castellano DESCARGA O PDF galego
Autor: Agustín Carrillo de Albornoz Torres, Onofre Monzó del Olmo, José María Sorando Muzás
Aplicaciones interactivas: José Luis Muñoz Casado
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
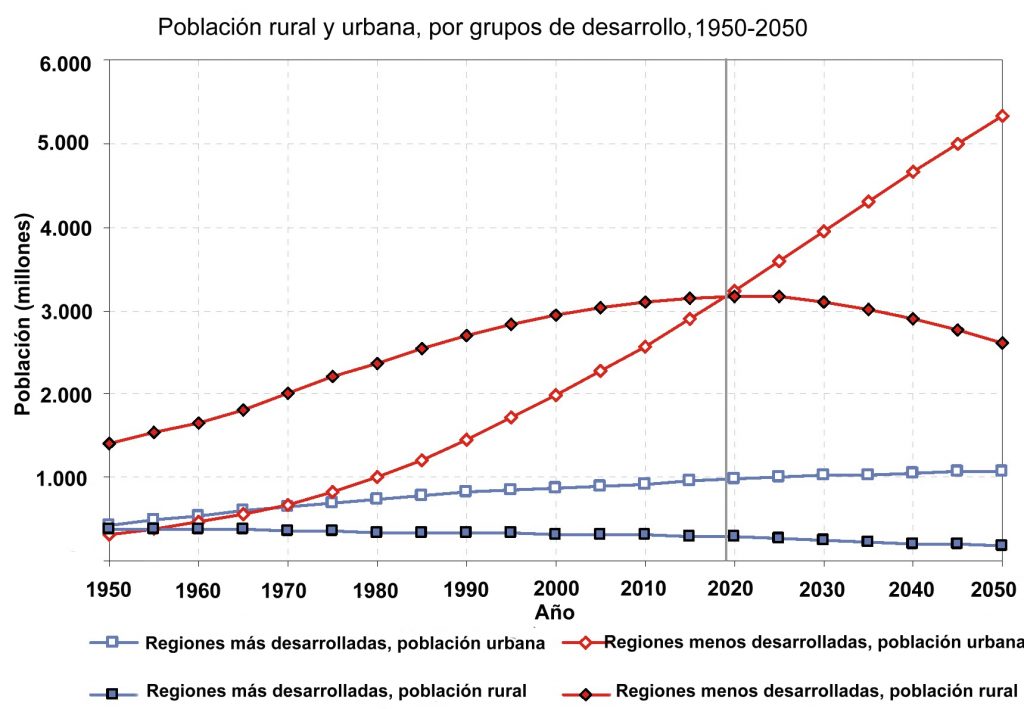
En 2008 la población urbana mundial había igualado a la población rural; y en 2015, aquella era un 54% del total. Esa situación ha evolucionado de forma desigual en las zonas más y menos desarrolladas. Así se refleja en las siguientes curvas, con extrapolaciones sobre el devenir futuro. De forma concisa y expresiva, el lenguaje de gráficas nos ayuda a comprender el mundo conocido y el que está por venir.
En un mundo cada vez más urbanizado surgen nuevos problemas y se necesitan soluciones viables, donde las matemáticas tienen mucho que aportar.
Urbanismo geométrico
La fundación o la planificación del desarrollo de una ciudad responden a una necesidad o a un propósito de tipo político, militar, económico o social.
Hay un problema que resolver con el trazado urbano y su solución es geométrica. A lo largo de la historia se han seguido varios modelos, a veces combinados.

Ciudad ortogonal
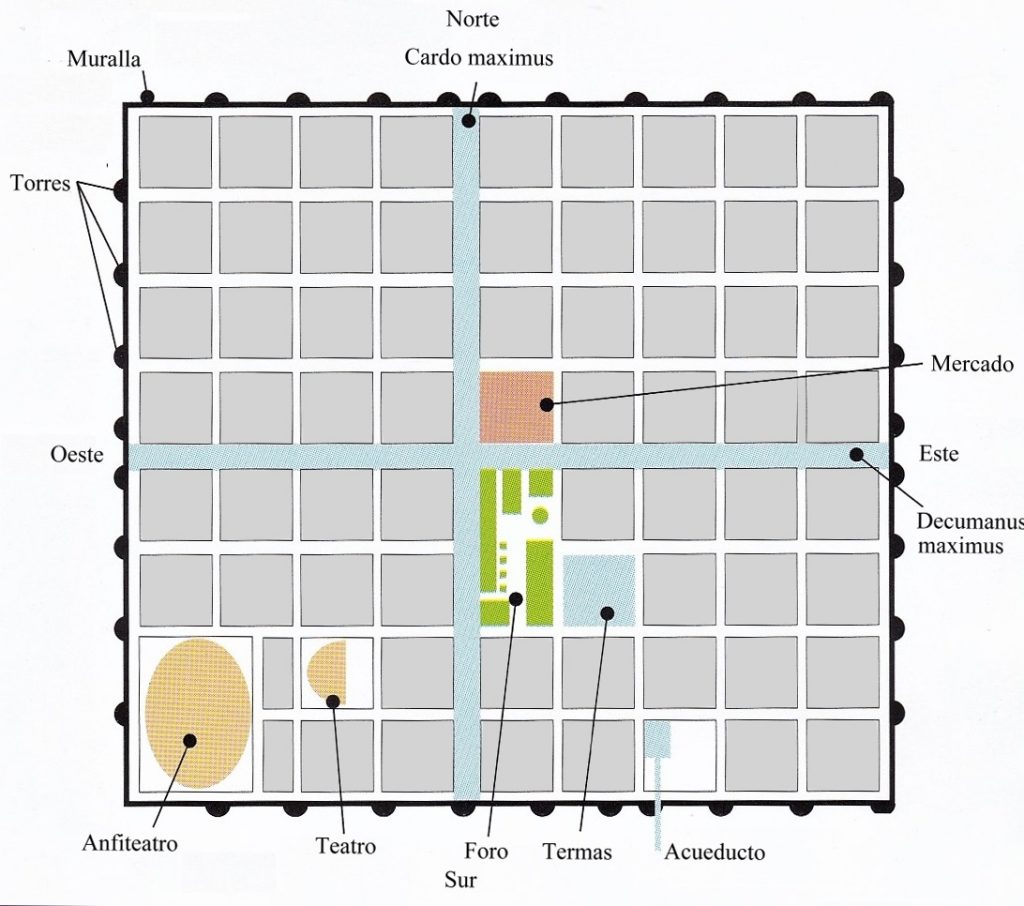
Las calles siguen dos únicas direcciones perpendiculares entre si y forman manzanas rectangulares, con frecuencia cuadradas.
El modelo ortogonal es el más extendido. En él, la distancia más corta entre dos puntos admite varios recorridos. Lo encontramos en
-
- Hipodamos de Mileto (s. V a.C.), primer urbanista conocido.
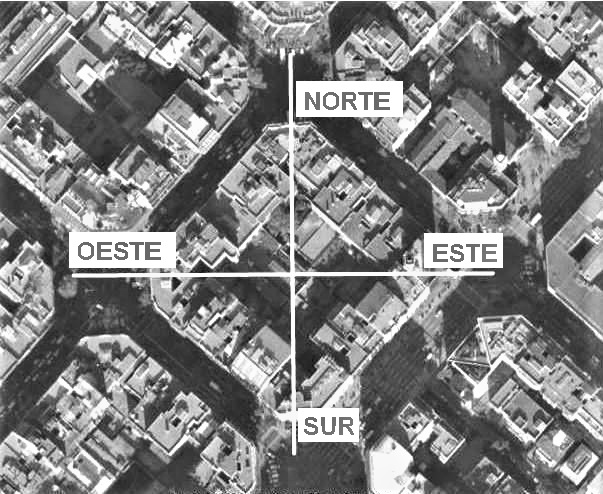
- Las ciudades con que consolidaba sus conquistas el Imperio Romano, cuya planta era un gran rectángulo con sus dos vías principales: el cardo (Norte-Sur) y el decumano (Este-Oeste), según el modelo de la capital, para así “vivir como en Roma”.
- Las ciudades hispanoamericanas, con la Plaza de Armas en el centro.
- Los ensanches de las ciudades europeas (s. XIX), como en L´Eixample de Barcelona, según el Plan Cerdá.
Ciudad radioconcéntrica
Con planta circular, desde la plaza central parten vías radiales enlazadas por calles concéntricas.
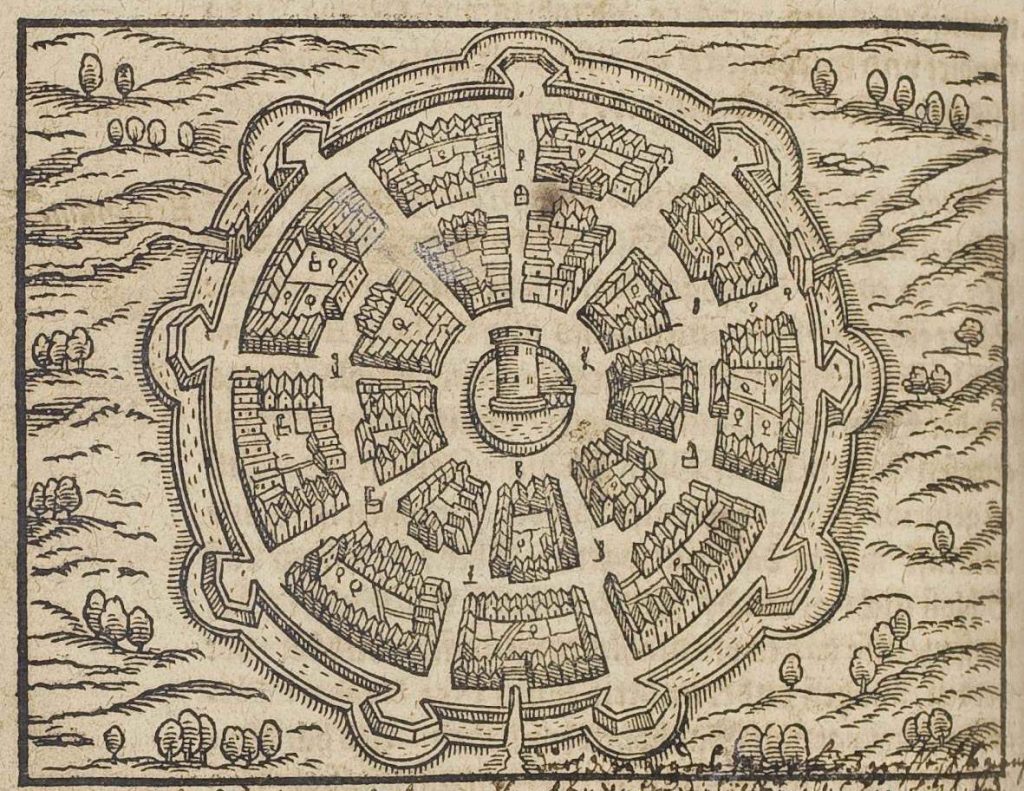
Aparece en varias épocas, desde la antigua Mesopotamia hasta modernas urbanizaciones exclusivas.
La distancia del centro a la periferia es mínima.
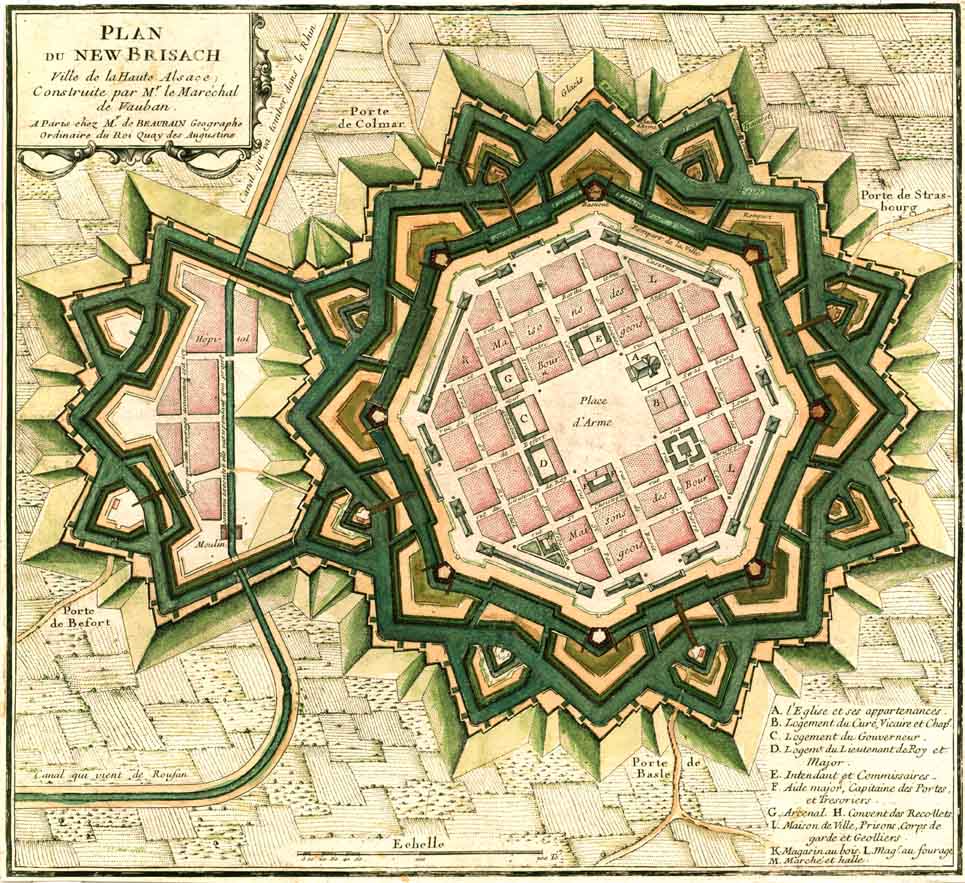
Ciudad estrellada
En el siglo XVII, para defender las fronteras se edificaron en Europa ciudades con forma de polígono rodeadas por murallas y fosos con forma de estrella.
Los bastiones en sus puntas eran diseñados por matemáticos estudiando la estructura óptima para la defensa artillera.
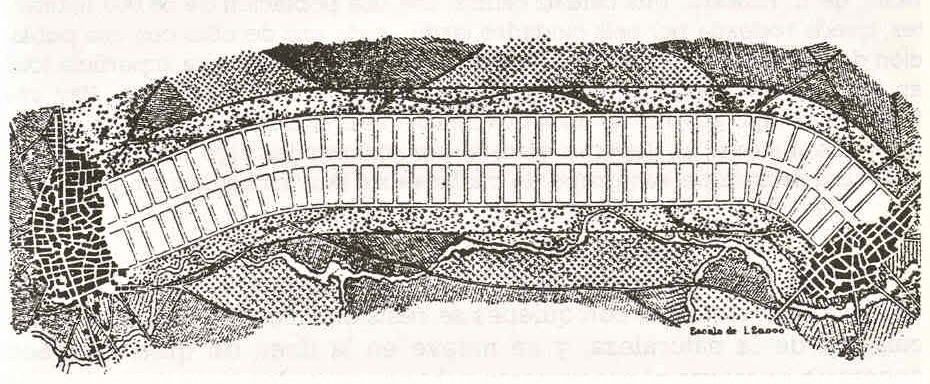
Ciudad lineal
Se desarrolla a lo largo de una vía de comunicación (un río, una carretera, etc.).
Arturo Soria proyectó en 1882 el crecimiento urbano lineal, uniendo las ciudades ya existentes. Fue aplicado brevemente en Madrid.
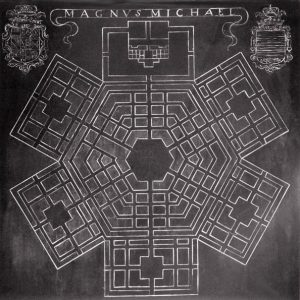
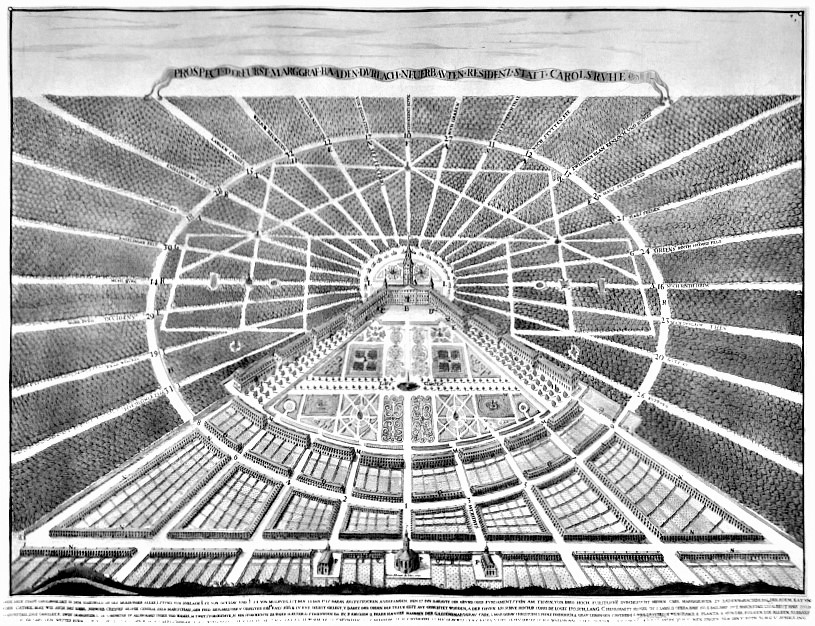
Otras ciudades geométricas
Hay ciudades con trazados geométricos diferentes a los anteriores. Por ejemplo:
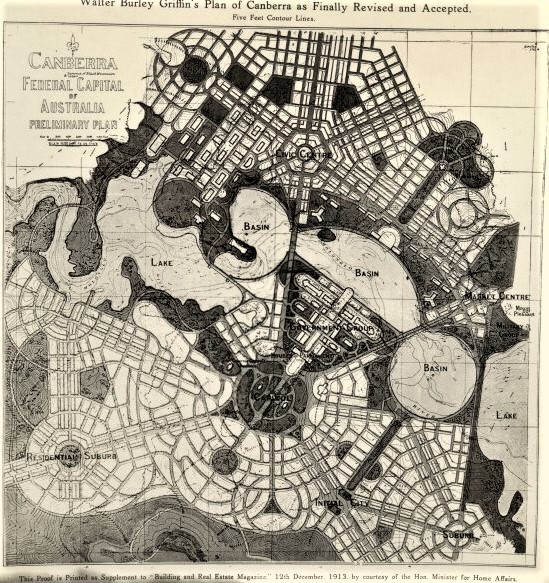
Geometría urbana para una vida mejor
La geometría urbana puede favorecer la calidad de vida.
- Ildefonso Cerdá orientó las manzanas de l´Eixample de modo que todas las fachadas recibieran las mismas horas de luz solar. Y trazó calles rectilíneas e iguales, sin un centro urbano, para igualar el valor de las viviendas.
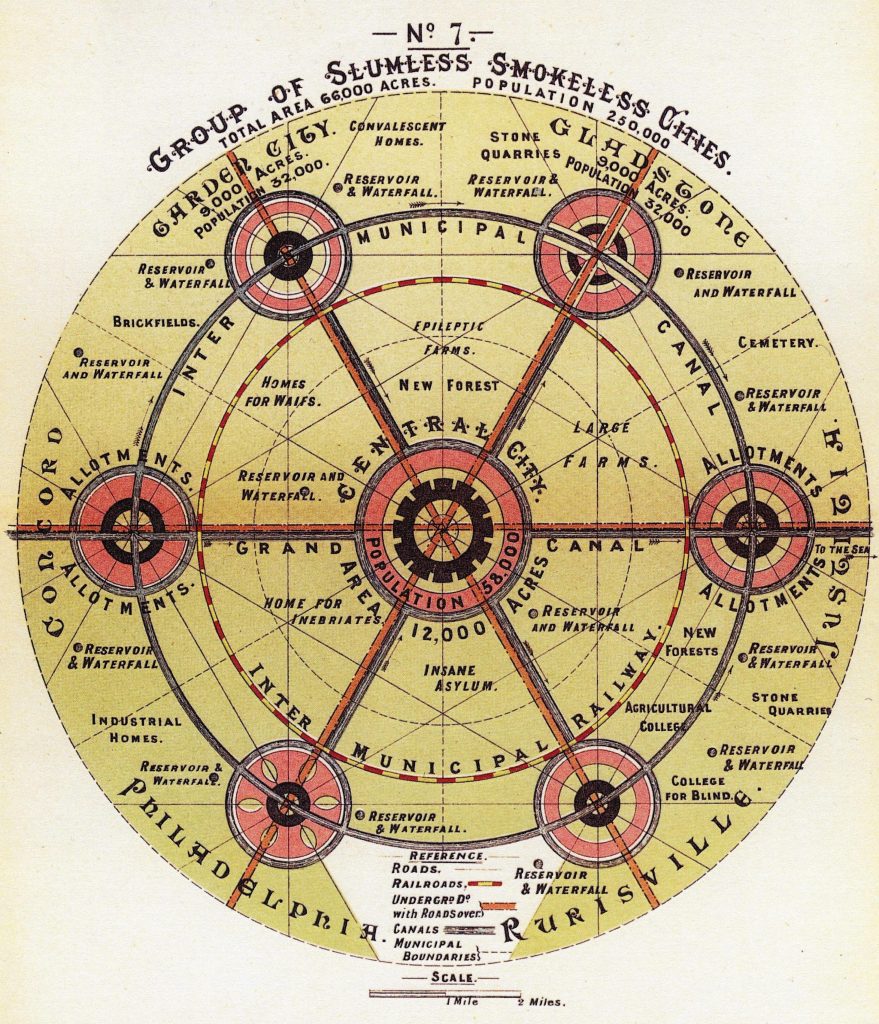
- Arturo Soria pretendía con la Ciudad Lineal acercar a los ciudadanos los beneficios de la vida en el campo, al igual que Ebenezer Howard con la Ciudad jardín (1902). En esta, alrededor de la gran ciudad crecían comunidades satélite circulares en contacto con la naturaleza.
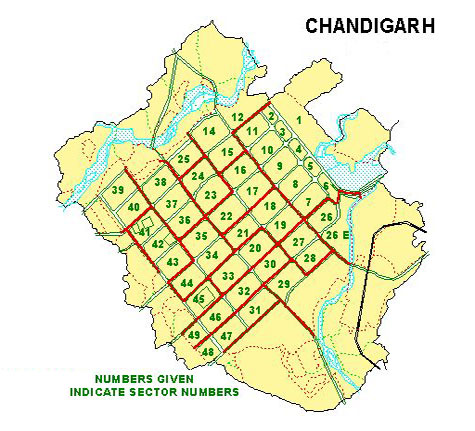
- Le Corbusier diseñó en India la ciudad de Chandigarh (1950), parcelada en sectores numerados de modo que cualquier persona pueda llegar caminando en 10 minutos a la escuela, al mercado, al médico, al templo o al parque. Es el hoy llamado cronourbanismo.
Muchos detalles matemáticos te esperan al pasear por tu ciudad. La aplicación MathCityMap te invita a descubrirlos en otros lugares del mundo.
Geometría a pie de calle
¿Por qué las tapas de las alcantarillas son redondas?
Alguna vez os habéis fijado en que las tapas de las alcantarillas son redondas. Os habéis preguntado el por qué.


Por los registros del alcantarillado han de poder bajar los empleados que se encargan de su revisión y limpieza. Y hay que evitar que cuando están en su interior la tapa se les caiga encima.
¿Por qué una tapa redonda no se puede caer por el agujero que deja?
Y aquí es donde aparecen las matemáticas. Si llamamos anchura de una figura plana a la distancia que hay entre dos puntos opuestos de su borde, se cumple que el círculo es de anchura constante, ya que la distancia que hay entre dos puntos opuestos de su borde (la circunferencia exterior) es siempre la misma, el diámetro.
Si la tapa fuera, cuadrada o rectangular, la diagonal es mayor que cualquiera de sus lados. Con lo que se podría colar si cae por esta.
Sin embargo, seguro que recordáis que habéis visto muchas tapas que no son redondas. Pero estas no son tapas de alcantarilla, habitualmente lo son de alumbrado, tomas de agua para los bomberos, telefonía…Y no suelen tener mucha profundidad y desde luego no cabe una persona.
Otro motivo es su peso, se pueden llevar rodando… y son más sencillas de encajar que si tuvieran cualquier otra forma.
Simetrías
La simetría es un concepto sencillo al cual podemos llegar observando el mundo que nos rodea.
Mirando nuestro cuerpo, los reflejos de las cosas, las formas vivas y las inanimadas, las trayectorias y las creaciones artísticas, pronto descubrimos unos principios de repetición que podemos organizar e incluso formalizar con unos mínimos conocimientos geométricos. La geometría nos habla de cómo la repetición de un movimiento genera una figura o una configuración a partir un motivo, y de cómo distintos tipos de movimientos generan figuras diferentes a partir del mismo motivo inicial: un juego sutil e ingenioso que, creando simetría, crea estructura y belleza.
Cuando miramos unas figuras geométricas, planas o espaciales, a simple vista tenemos una sensación de qué figura es más simétrica. La geometría nos proporciona una forma más precisa de ver y clasificar el tipo de simetría de las figuras y las configuraciones: una simetría de una figura es un movimiento que hace que la figura coincida consigo misma.
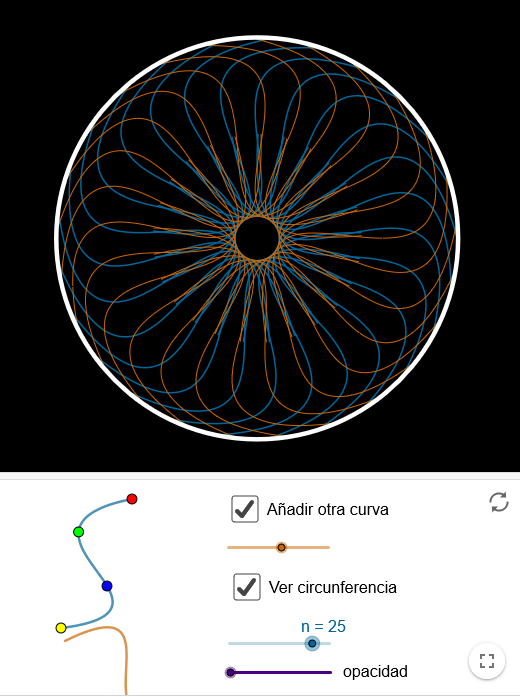
Simetrías en los rosetones
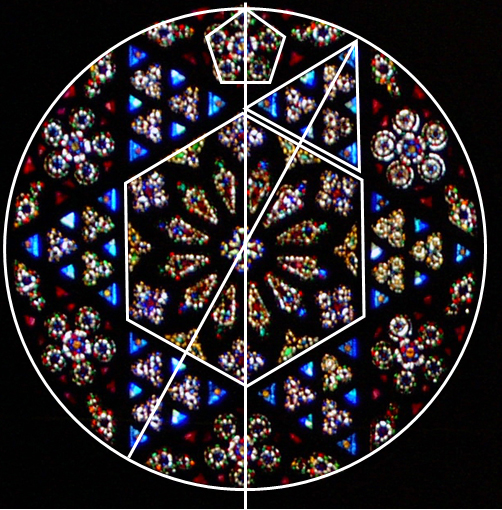
Leonardo da Vinci se dio cuenta de que había dos tipos diferentes de rosetones, unos sin simetría de reflexión (rosetones cíclicos) y otros con simetría de reflexión (rosetones diédricos).
Si se hace girar un rosetón alrededor de su centro hasta completar una vuelta, coincide con la posición original cada 360º/n. Una simetría cíclica no tiene rectas de simetría (espejos), pero una simetría diédrica tiene n rectas diferentes de simetría. Las notaciones respectivas para estos diseños son cn y dn.


El molinete de viento tiene una simetría cíclica (c7) y la flor, diédrica (d5).
Además de en las iglesias, es frecuente encontrarnos con rosetones muy cerca de nosotros: las llantas y los tapacubos de los coches.


Puedes construir tus propios rosetones con este applet.
Frisos
En arquitectura un friso es la parte del entablamento comprendida entre el arquitrabe y la cornisa. Pero habitualmente llamamos friso a:
- Una decoración esculpida, pintada o grabada en bandas horizontales.
- Faja que contrasta por el dibujo o el color y adorna y rodea una extensión de fondo.
- Faja más o menos ancha que se suele pintar a la parte inferior de las paredes, de diferente color que estas.

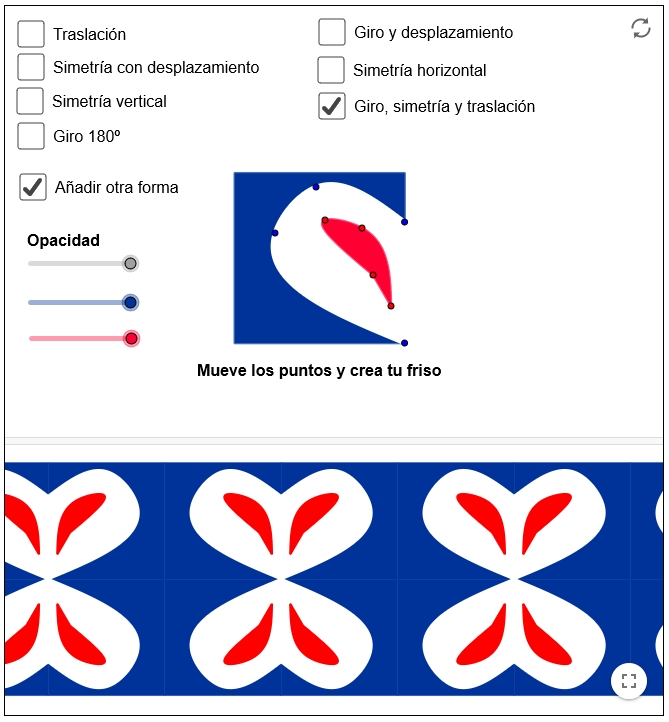
En matemáticas lo que caracteriza a los frisos es que están generados, a partir de una figura, por un conjunto de isometrías que tienen la propiedad que hay una recta a la que todas las isometrías de ese conjunto la dejan invariante. Por eso es por el que los frisos se quedan en una franja del plano. Los solemos encontrar en balcones, encima de algunos dinteles…


- Friso generado por una simetría horizontal y traslación.

- Friso generado por una simetría vertical y traslación.
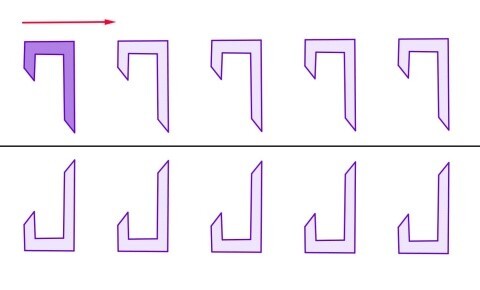
- Friso generado por una simetría en deslizamiento y traslación.
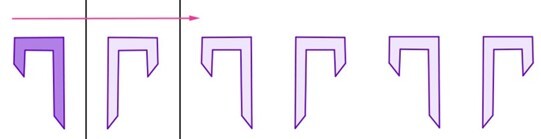
- Friso generado por un giro de 180º y traslación.
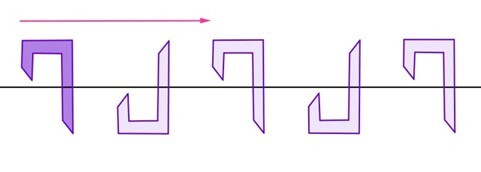
- Friso generado por una simetría vertical, una horizontal y traslación.
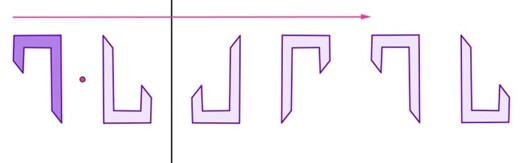
- Friso generado por un giro, una simetría vertical y traslación.
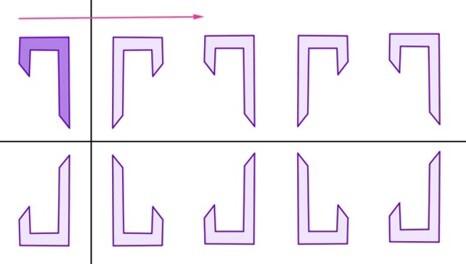
Con este applet puedes diseñar tus propios frisos:
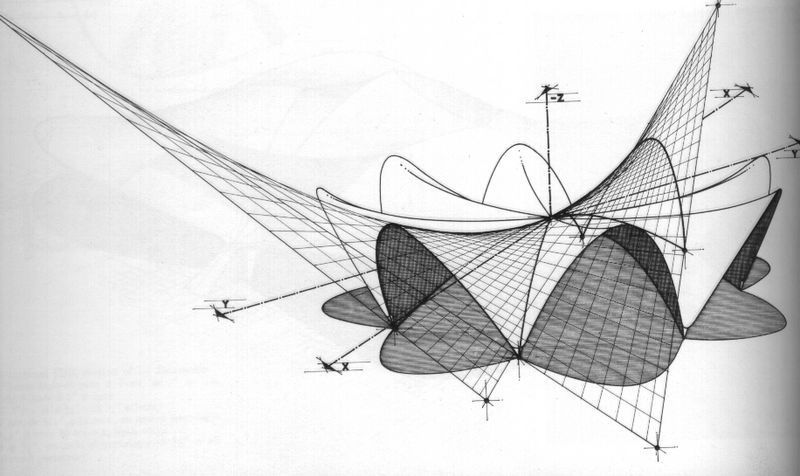
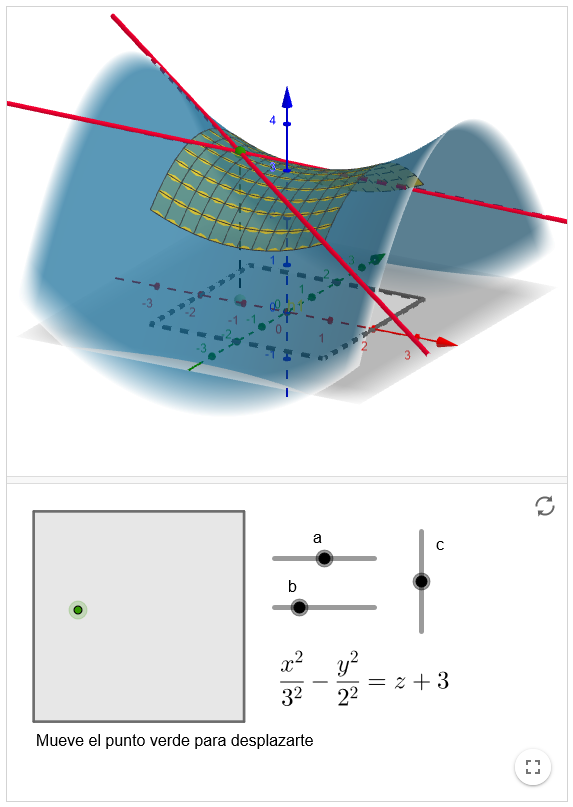
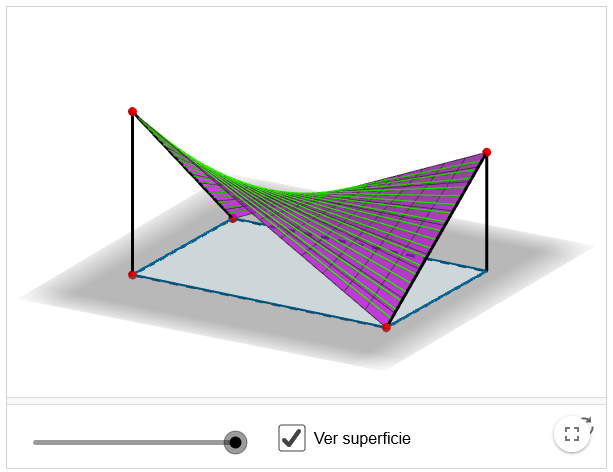
Superficies regladas
Las superficies regladas son muy importantes en arquitectura ya que permiten construir estructuras curvas mediante rectas.
Para construir este tipo de superficies con rectas (los tablones del encofrado), solo hay que hacer variar el ángulo de inclinación de una recta que se mueve sobre otra curva.
Si te acercas a este tipo de construcciones podrás ver las marcas de los tablones (rectas) de los encofrados.
Si te acercas a este tipo de construcciones podrás ver las marcas de los tablones (rectas) de los encofrados.
Obsérvalos en cualquier construcción que utilice hormigón.