¿Sabías que…?

¿Sabías que…

… tus deportivas se diseñan utilizando matemáticas?

DESCARGA

Diversas empresas del sector del calzado sanitario y deportivo colaboran con especialistas en matemáticas para analizar la calidad final de sus productos. Para ello se utilizan modelos matemáticos complejos que, traducidos al lenguaje de un ordenador, permiten predecir el confort y calidad de un diseño a partir de su geometría y de las propiedades térmicas de los materiales utilizados en su fabricación.

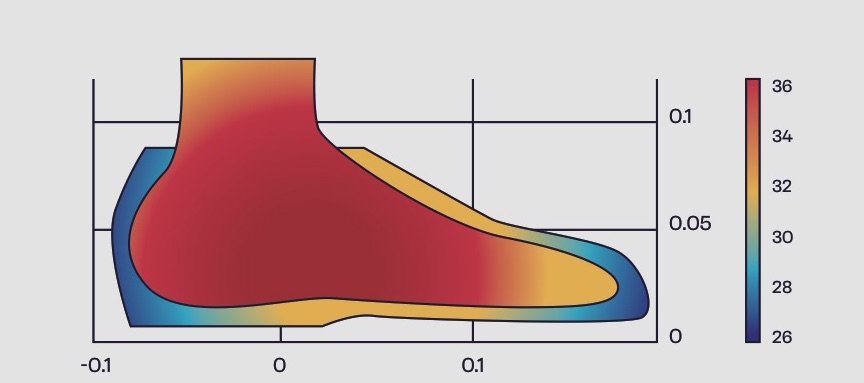
Esto permite a la empresa reducir enormemente los tiempos de la fase de diseño y desarrollo del producto, pues se evitan por un lado la fabricación de diferentes prototipos físicos y por otro el ensayo en laboratorio con distintos materiales. De este modo, es posible incrementar la calidad final del producto reduciendo su coste. Además, con esta simulación virtual, se reduce el impacto medioambiental del proceso gracias al ahorro de materiales y energía de fabricación de los diferentes prototipos.

Cortesía de: J. Durany, L. Poceiro y F. Varas (Universidad de Vigo)

Para saber más: http://cedya2015.uca.es/cedya2015proceedings/

¿Sabías que…

… se puede cambiar la válvula aórtica usando matemáticas?

DESCARGA

La estenosis aórtica es una enfermedad que provoca un funcionamiento incorrecto de la válvula aórtica, obligando a que el corazón haga un sobreesfuerzo y derivando en complicaciones mayores, casos en los que se aconseja el recambio valvular. Además de la operación a corazón abierto, es posible cambiar la válvula accediendo a los órganos interiores a través de un catéter, técnica conocida por TAVI (Transcatheter Aortic Valve Implantation). La intervención presenta diversos retos como la selección del tipo y tamaño de dispositivo adecuados, la presión adecuada en su colocación, etc.

Gracias a las técnicas de simulación numérica es posible realizar de forma virtual diversas TAVI a un mismo paciente. De este modo, pueden predecirse posibles complicaciones durante la intervención, así como las modificaciones en la válvula nativa del paciente o las tensiones a las que estará expuesto el anillo aórtico durante el procedimiento.

¿Sabías que…

… las matemáticas permiten caracterizar una población?

DESCARGA

El estudio de los apellidos, usado tradicionalmente para el conocimiento de la estructura genética de las poblaciones, se emplea hoy día para la caracterización de los habitantes de una región. Utilizando herramientas estadísticas, es posible analizar los patrones observados en la distribución de los apellidos y extraer datos sobre los movimientos y características de las poblaciones, y así estudiar las relaciones con otros factores (historia, lengua, genética, demografía, etc.). Algunos son términos dotados de valor semántico, que reflejan realidades y conceptos, y que el tiempo ha convertido en apellidos. Por ejemplo, en Galicia, abundan los apellidos que coinciden con el nombre de partes de la anatomía humana (Pernas (3.320), Cabeza (650), Cabello (226)), con características físicas o morales de la persona (Calvo (12.747), Justo (2.742)) o nombres relacionados con el campo (Pereira (de peral) (24.838), Romero (19.884)).

Cortesía de: María José Ginzo-Villamayor (Universidade de Santiago de Compostela)

Para saber más: http://eamo.usc.es/pub/mjginzo

¿Sabías que…

… las matemáticas pueden ayudarte a salvar tus inversiones?

DESCARGA

En los últimos años, ciertos tipos de interés de referencia en las operaciones financieras se han vuelto negativos. Por ejemplo, el tipo de interés interbancario EURIBOR cotiza por debajo de cero. Si contratas un depósito que remunera a un tipo negativo, deberías pagar por tener dinero en el banco en lugar de recibirlo, aunque también casi nos tendría que pagar el banco por nuestra hipoteca. Como tradicionalmente esto nunca ha ocurrido, los modelos matemáticos para valorar productos que dependen de estos tipos de interés han tenido que modificarse, así como los modelos de evolución de los propios tipos de interés. No obstante, las matemáticas han “aguantado el tipo”. Complejas herramientas matemáticas, algunas usando nuevos tipos que se obtienen sumando cantidades adecuadas a los tipos negativos y modelando sus dinámicas, permiten dar solución a estas coyunturas financieras. Algo parecido ha ocurrido con ciertos precios de determinado barril de petróleo que se han vuelto negativos, debido a la bajada de consumo de carburante durante la crisis del covid-19. Esto ha sido “gasolina” para hacer matemáticas.

¿Sabías que…

… se utilizan matemáticas para diseñar los “brackets”?

DESCARGA

Los aparatos dentales conocidos como “brackets” se han convertido en elementos imprescindibles para la corrección de los dientes. Constan de una placa que se fija al diente con una estructura de pestañas a ambos lados de una hendidura por la que pasa un alambre ajustado. Aplicando distintas fuerzas al alambre y enlazando las pestañas se consigue transmitir al diente cargas en distintas direcciones que lo mueven según se desee. Es frecuente la ruptura por sobresfuerzo de las pestañas o del propio alambre. Utilizando modelos matemáticos es posible simular el comportamiento de la estructura y mejorar su diseño y prestaciones. En el futuro será posible combinar esta simulación del aparato con nuevos modelos de movimiento de manera que será posible predecir los efectos de un tratamiento en cada paciente.

Cortesía de: Juan Viaño (Universidade de Santiago de Compostela)

Para saber más: Boletín SeMA 33 (2015) https://www.sema.org.es/es/publicaciones/boletin-electronico-sema

¿Sabías que…

… Suiza ganó la Copa América de vela gracias al uso de las matemáticas?

DESCARGA

Hace no muchos años, la mejor forma de probar el rendimiento de un barco era exponerlo a situaciones de flujo realistas en túneles de viento o tanques. Actualmente, utilizando modelos matemáticos complejos y convenientemente traducidos a un ordenador es posible simular la respuesta del barco bajo distintas condiciones. En particular, se puede mejorar el diseño del yate para que se mueva por el agua con la menor resistencia posible u obtener nuevas formas de velas que contrarresten mejor la deformación que sufren por la interacción con el aire. Pero, además, pueden hacerse modelos para ayudar al navegante a tomar decisiones, como cuando dos barcos van juntos y uno cambia de dirección. Un equipo de matemáticos aplicó todas estas técnicas al barco suizo Alinghi, probando más de 50 diseños que se ejecutaban en potentes ordenadores durante más de diez horas de cálculos cada diseño. Y lo consiguieron: Suiza, país sin costa oceánica, ganó la Copa América en los años 2003 y 2007.

Cortesía de: Alfio Quarteroni (Politecnico di Milano, Italia y EPFL, Suiza)

Para saber más: https://people.epfl.ch/alfio.quarteroni

¿Sabías que…

… las matemáticas son fundamentales en la predicción de tsunamis?

DESCARGA

Las matemáticas son la base de los modelos que se utilizan para la simulación numérica de flujos geofísicos. Así, a partir de unos datos precisos del terreno, estos modelos matemáticos son capaces de mostrarnos desde la inundación que puede producir el desbordamiento de un río, hasta la dinámica del mar de una zona costera o incluso predecir el tiempo de impacto de una onda de tsunami y la altura con que la ola va a llegar a determinada zona costera.

En estos últimos casos, los modelos matemáticos combinan algoritmos numéricos robustos, es decir, que no son sensibles a los pequeños cambios en los datos de entrada, con hardware GPU (Graphic Processor Units) de última generación para poder simular con detalle el tsunami y sus efectos en cuestión de minutos y así ayudar a las autoridades encargadas de velar por nuestra seguridad de poderosas herramientas hasta ahora impensables.

Cortesía de: Grupo EDANYA (Universidad de Málaga)

Para saber más: https://edanya.uma.es/hysea/index.php

¿Sabías que…

…multitud de paisajes de películas se generan por ordenador usando fractales?

DESCARGA

La palabra fractal fue acuñada en los años 70 para describir objetos matemáticos cuya estructura se repite a distintas escalas o que son extremadamente rugosos. La clave de su versatilidad reside en que una única orden puede, sin más que repetirla muchas veces, dar lugar a objetos de apariencia muy compleja. Los fractales supusieron un cambio de paradigma dentro de las matemáticas, que permitió modelizar complejos elementos y procesos de la naturaleza. Por este motivo tienen aplicaciones en medicina, biología, geología, telecomunicaciones, economía o compresión de imágenes digitales, entre otras.

Los fractales han sido utilizados en la industria cinematográfica. Están detrás de la generación digital de árboles u otras plantas, de montañas o nubes y de una variedad de objetos fantásticos. Star Trek 2: La ira de Khan (1982) fue la primera película en la que se utilizaron para generar un paisaje realista, pero su uso se extiende a muchas otras películas, como Guardianes de la galaxia, vol. 2 (2017) para crear el planeta de Ego o Aniquilación (2018), en la cual el fractal Mandelbulb (en la imagen) sirvió para representar a un alienígena.

¿Sabías que…

… los nudos pueden ayudar a curar enfermedades?

DESCARGA

El ADN (ácido desoxirribonucleico) es una gran molécula que almacena nuestro código genético; gracias a él, se produce la transmisión hereditaria (información sobre cómo producir proteínas, color de los ojos, predisposición a ciertas enfermedades, …)

Una molécula de ADN consiste en dos cadenas que se enrollan entre ellas formando una doble hélice, y una serie de “peldaños” que las conectan, dándole la forma de escalera de caracol. Sucede que, en ocasiones, el ADN está superenrollado (de manera parecida a los cables de los teléfonos antiguos), lo que hace difícil que tengan lugar ciertos procesos indispensables para la vida. Para ello, el organismo dispone de topoisomerasas, enzimas que manipulan y desenredan las cadenas. Para lograr entender la acción de una enzima, se aísla y se deja que actúe sobre el ADN, observando la forma en que ha quedado anudado. Ahora bien, ¿cómo determinar la acción de la enzima sin más que mirar la forma en que ha quedado anudada la hélice?

Es aquí donde interviene la Teoría de Nudos, una rama de las matemáticas que se encarga de estudiar las transformaciones que pueden hacerse a los nudos (pensamos en un nudo matemático como una cuerda que atamos y en la que pegamos sus extremos entre sí). Las técnicas del álgebra y la topología y los invariantes de nudos que proporciona esta rama contribuyen a la comprensión de la acción de ciertas enzimas, lo que resulta crucial en el estudio de algunas enfermedades.

¿Sabías que…

… hay ecuaciones que nos dicen cuándo sacar el paraguas?

DESCARGA

Hasta el siglo XIX, las predicciones de muchos fenómenos se basaban en anotar los datos observados durante años y buscar patrones que permitieran intuir algún pronóstico para un futuro cercano. La idea era sencilla, sin embargo, las predicciones así obtenidas no eran muy efectivas. En la actualidad, el modelado matemático permite hacer predicciones con gran fiabilidad. Un modelo  matemático es una representación simplificada, mediante ecuaciones matemáticas, de un determinado fenómeno. Así, podemos estudiar fenómenos naturales, físicos o sociales, permitiéndonos hacer pronósticos o evaluar las consecuencias de una determinada actuación. Un ejemplo sería el estudio de la predicción del tiempo atmosférico. Para modelar un fenómeno tan complejo, el primer paso sería determinar las variables que influyen en él, y cómo se relacionan entre sí (teniendo en cuenta ciertas leyes físicas). Es en este punto donde aparecen las ecuaciones diferenciales, igualdades en las que se relaciona una función con sus derivadas.

Así, las funciones vendrían a representar las cantidades físicas (temperatura, presión…) y las derivadas sus tasas de cambio. Cuanto mayor sea la exactitud al resolver estas ecuaciones, mejor será la precisión en la predicción atmosférica.

¿Sabías que…

… para saber la edad de las regiones lunares se usa una escala logarítmica?

DESCARGA

Las imágenes de superficies planetarias obtenidas por las sondas enviadas al espacio, o de la Luna, permiten relacionar el tamaño y la distribución de los cráteres en una región determinada con su edad geológica. La idea se basa en que la cantidad de impactos recibidos en la superficie, y que han producido los cráteres, ha disminuido exponencialmente con el tiempo.

La datación de la edad geológica mediante el conteo de cráteres es un ejemplo de escala logarítmica, como también lo son la escala de Richter para terremotos, el pH de ácido-base, los decibelios, la luminosidad de las estrellas, la evolución de poblaciones o epidemias (como la Covid-19), la desintegración radiactiva, etc.

Una escala logarítmica permite visualizar cantidades que crecen exponencialmente, como puede ser la intensidad de un terremoto, mediante valores que crecen linealmente, como son las magnitudes en la escala Richter. Así, un terremoto de magnitud 3 es 10 veces más intenso que uno de magnitud 2 y también es 10 veces menos que uno de magnitud 4.

¿Sabías que…

… las bolsitas de té piramidales son las más adecuadas?

DESCARGA

 Mejorar la experiencia de los 100 millones de consumos diarios de té en Reino Unido hizo que los investigadores de una conocida marca se replantearan el diseño de sus bolsitas. Dieron el salto pasando de dos a tres dimensiones tratando de conjugar varios factores: economizar el material, una fácil fabricación, almacenamiento más eficiente y que fuese de diseño atractivo. La forma elegida resultó ser un tetraedro, formado a partir de 4 triángulos equiláteros, que se puede construir fácilmente, como las bolsas planas, con únicamente dos cierres (en este caso girados 90 grados), pero proporcionando un mayor volumen.

El primer envase moderno con esta forma fue el tetrabrik original (Tetra Classic, 1952) para envasar líquidos –aunque el tetrabrik actual es un paralelepípedo–, además hoy en día se utiliza este diseño con forma de tetraedro para muchos otros productos (granulados como el azúcar, aperitivos, etc).

¿Sabías que…

… escuchas música gracias a la transformación matemática de los sonidos?

DESCARGA

Cuando se realiza una grabación digital de música, los sonidos son descompuestos en sus distintas frecuencias (o notas musicales) y amplitudes (o volumen). De esta forma, los sonidos se transforman y almacenan como un listado de números. La transformación recibe el nombre de transformada de Fourier. Esta representación matemática permite toda clase de manipulaciones sobre la señal (es decir, sobre el listado de números almacenados), como es el comprimirla, filtrarla, quitar ruidos, añadir efectos, elaborar apps de reconocimiento de canciones, etc. Posteriormente, la transformada de Fourier inversa será la que permita su reproducción en cualquier dispositivo digital (móvil, reproductores mp3, etc).

El mismo principio se utiliza en el tratamiento de imágenes digitales donde ahora son los colores los que son transformados en números, siendo posible también el manipularlos para poder realizar compresión (en formato jpg, png y otros), filtros, efectos, restauración, etc.

¿Sabías que…

… los números primos guardan tus secretos?

DESCARGA

Cuando enviamos información por internet (por ejemplo, al comprar con una tarjeta de crédito), corremos el riesgo de que sea interceptada. Por eso, para que sea transmitida de forma segura debemos cifrar la información antes de enviarla, utilizando un código que sólo conozca la persona destinataria, para que nadie más pueda descifrar el contenido del mensaje.

Pero, ¿cómo podría un banco acordar un código de cifrado secreto con cada uno de sus clientes? Es aquí donde entran en juego las claves públicas, que son códigos de cifrado que tienen dos partes: una parte visible para todos los clientes que sirve para cifrar el mensaje antes de enviarlo y una parte privada, que sólo conoce el banco, y que permite descifrar el mensaje recibido. Ésta es la base sobre la que funcionan los métodos actuales de encriptación.

Uno de estos métodos es el algoritmo RSA. La clave privada son dos números primos (es decir, que sólo puedan dividirse por 1 y por ellos mismos) y la clave pública el producto de ambos. Si, por ejemplo, la clave pública es 187, podemos deducir sin demasiado esfuerzo que los números 11 y 17 constituyen la clave privada (porque 187 = 11 ´ 17). Pero si usamos números lo suficientemente grandes, encontrar la clave privada se vuelve un problema imposible hasta para los ordenadores más potentes que tenemos hoy en día.

¿Sabías que…

… los filtros aplicaciones como Instagram utilizan matemáticas?

DESCARGA

Cualquier imagen digital —sea de una pantalla de ordenador o de un móvil— es una región cuadrada o rectangular dividida en franjas horizontales y verticales formando una cuadrícula. Cada una de las pequeñas regiones cuadradas de la misma recibe el nombre de pixel (acrónimo de picture element). Si la imagen es en blanco y negro, cada pixel lleva asociado un valor numérico entre 0 y 255 (la intensidad de color de cada pixel está codificado en un byte, una expresión binaria de 8 dígitos –8   bits–, luego existen 2⁸ = 256 posibilidades), obteniéndose así una cuadrícula de números, que en matemáticas se llama “matriz”. Para imágenes en color, por ejemplo, el modelo RGB, se generan tres matrices correspondientes a los valores, entre 0 y 255, de intensidad de los colores rojo (Red), verde (Green) y azul (Blue).

Las aplicaciones de nuestros teléfonos móviles, cámaras digitales u ordenadores relacionadas con el procesamiento digital de imágenes utilizan algoritmos que modifican los valores de las matrices de números asociadas a la imagen con el objetivo de mejorar la calidad de la misma, añadir efectos (como los filtros de Instagram), restaurar la imagen, facilitar la búsqueda de información, realizar reconocimientos de expresiones faciales, etc.

¿Sabías que…

… los códigos de barras fueron inventados para evitar colas en los supermercados?

DESCARGA

 En 1949, Norman Woodland tuvo una idea brillante para solucionar el problema que empezaban a generar las largas colas que se formaban en los primeros grandes supermercados americanos. En lugar de obligar al cajero a introducir el nombre y precio de cada uno de los productos, se creó un código numérico cuyas cifras identificaban los distintos productos y sus precios. Presentó esta información con barras blancas y negras fáciles de leer para un lector óptico-eléctrico conectado a un ordenador que podía elaborar la nota de la compra. Entre los sistemas de códigos de barras más extendidos está el código EAN-13, formado por un número de trece cifras: las dos o tres primeras identifican el país emisor, las cuatro o cinco siguientes identifican la empresa propietaria de la marca y las que faltan para llegar a doce identifican el producto. La última cifra, llamada dígito de control, que se calcula a partir de las doce primeras, y que da cierta seguridad a la lectura óptica.

El dígito de control es lo que falta para la siguiente decena a la suma de los números que están en lugar impar más tres veces la suma de los que ocupan lugar par. Por ejemplo, para 59-01234-12345 se calcula (5+0+2+4+2+4) + 3x(9+1+3+1+3+5) = 83 y el dígito de control sería 7.

En la actualidad, los códigos de barras son esenciales en almacenamientos, en logística de distribuciones, en exámenes anónimos, etc.

¿Sabías que…

… los telares influyeron en las computadoras?

DESCARGA

La idea original de un telar era disponer de un artilugio donde situar hilos paralelos tensados (urdimbres) y elevar con algún mecanismo estos hilos formándose una abertura (calada) a través de la cual pasar “la trama” de hilos. El primer telar de pedales data del siglo X. Pero fue Jacques Marie Jacquard (1752-1834) quien tuvo la genial idea de un telar automático, “programable” a partir de tiras articuladas de tarjetas perforadas.

A lo largo de la historia las laboriosas operaciones aritméticas fueron realizadas con la ayuda de ábacos y luego de tablas o reglas de cálculo. Sin embargo, una aproximación mecánica interesante fue dada por Charles Babbage (1791-1871) al diseñar la Máquina Analítica para ejecutar operaciones matemáticas complejas. Y fue el telar de Jacquard el que dio pie a un avance práctico y realista: copiar la idea de las tarjetas perforadas para el funcionamiento de las computadoras. En 1970 las tarjetas perforadas aún eran clave en la programación informática.

¿Sabías que…

… las matemáticas cambiaron el baloncesto?

DESCARGA

El baloncesto actual nada tiene que ver con el de épocas pasadas. Uno de los principales motivos es el uso del triple. La línea de tres puntos fue introducida en el baloncesto español en la temporada 1984/1985. Desde entonces el uso de este tipo de lanzamientos ha seguido una tendencia creciente a lo largo de los años, pasando del 7,5% de los tiros aquella temporada al casi 40% en la actualidad.

De hecho, en el año 2010 la FIBA decidió retrasar la línea de tres puntos de los 6,25 metros a los 6,75 actuales para recuperar el atractivo y dinamismo que estaba perdiendo el deporte con el abuso de este tiro. Sin embargo, los equipos han seguido apostando por la eficiencia de los triples porque las matemáticas confirman que cuantos más triples se anoten, más probabilidades de ganar existen.

Si se multiplica el porcentaje de canastas de los lanzamientos de corta distancia (1 – 3 m), 58,7%; media distancia (3 – 5 m), 35,3%; larga distancia (5 – 6,75 m) y triple, 36,3%, por los puntos de esas distancias (2 y 3 puntos), se observa que los puntos de media por jugada son mejores en corta distancia (1,17 puntos) y triple (1,09), que en las distancias media (0,7) y larga (0,78). En conclusión, lanzar de media distancia equivale a perder puntos.