DESCARGA EL PDF castellano DESCARGA O PDF galego
Autor: Rafael Losada Liste
Aplicaciones interactivas: Rafael Losada Liste y José Antonio Mora Sánchez
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- ¿Qué es una red?
- ¿Qué es un grafo?
- ¿Cómo y cuándo aparecen los grafos?
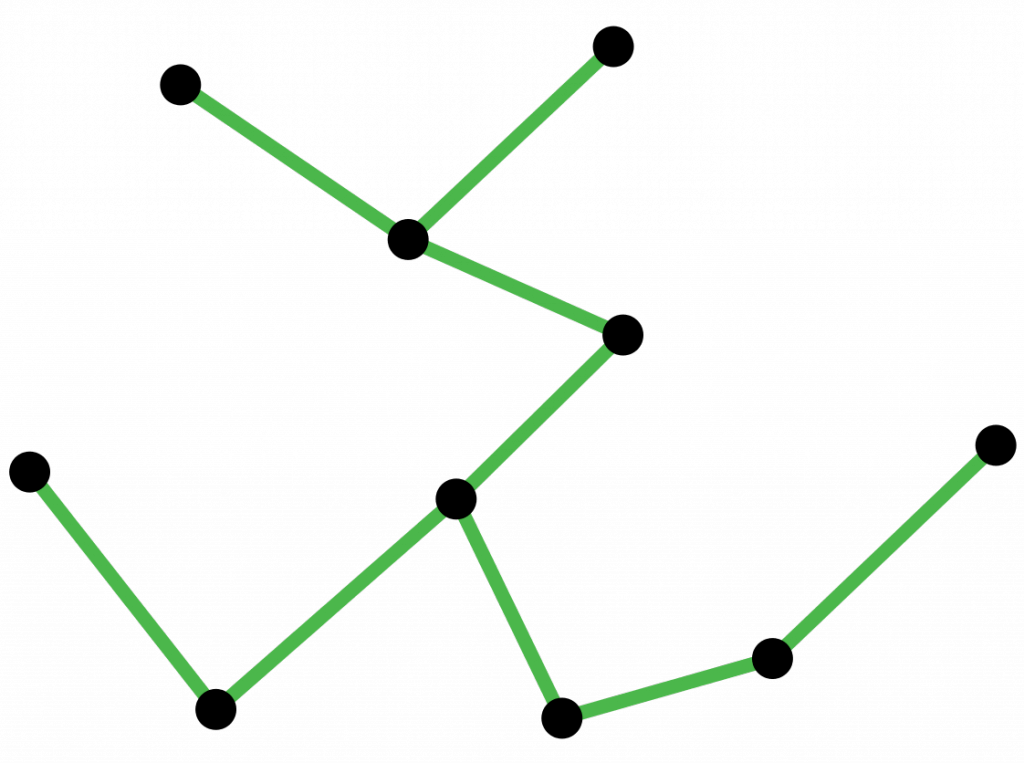
- Figuras de un solo trazo
- Grafos simples
- Lema del apretó de manos
- Regiones de proximidad
- Coloración de grafos
- Redes y grafos
- Árboles
- Aplicaciones de grafos
- Nodos de telefonía fija
- Número cromático
- Five Room puzzle
- Isomorfismo de grafos
- Grafos planos
- Esqueletos de los poliedros
- Caminos hamiltonianos
- Grafos completos
- Grafos bipartitos completos
- Matriz de adyacencia
- Número de caminos entre dos nodos
- Más actividades
- Bibliografía
Porque todo está conectado
En un mundo global como el actual, abundan las conexiones entre objetos, personas y organismos.
Estas conexiones forman a menudo una intrincada red cuyo análisis es fundamental para optimizar su funcionamiento y resolver problemas.
Los modelos matemáticos de estas redes se fundamentan en la Teoría de Grafos. Un grafo no es más que un esquema de las conexiones de una red.
Esta exposición te ayudará a sumergirte en el mundo de las redes y los grafos a través de diversos ejemplos y actividades que, de forma muy simplificada, recogen algunos términos y principios básicos.
¿Qué es una red?
Piensa en las personas que conoces y te conocen, con las que hablas a menudo. Con cada una de ellas tienes una conexión, algo que no pasa con las demás personas. Pero, a su vez, cada una de esas personas, no solo te conoce a ti, conoce a otras, ya sean conocidas tuyas o no.

A medida que empieces a expandir esta cadena de conocidos, surgirán más y más personas que tú no conoces directamente, pero con las que podrías comunicarte si supieses cuáles son las personas intermedias que te separan de ellas.
Entre todas esas personas hay entonces una gran cantidad de conexiones, la gran mayoría de ellas desconocidas para ti. Decimos que el conjunto de todas esas personas y sus conexiones forman una red (en este caso, una red social).
Si cambiamos las personas por ciudades y los reconocimientos por carreteras, obtenemos una red de carreteras. Si hablamos de teléfonos fijos y cables telefónicos obtenemos una red telefónica. Hay montones de cosas, personas, instituciones, hechos, símbolos, etc. que pueden interconectarse de diferentes modos. Cada uno de esos conjuntos de conexiones forma una red.
¿Qué es un grafo?

Los grafos expresan las conexiones existentes en una red. Con el paso de los años, la Teoría de Grafos ha ido generando tantas aplicaciones que hoy se usa prácticamente en el análisis de cualquier red.
¿Cuándo y cómo aparecen los grafos?
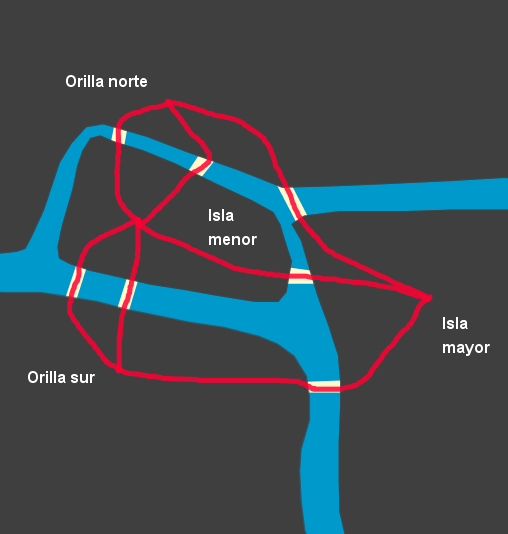
Comparativamente con otras áreas matemáticas, los grafos son bastante recientes. Surgen a partir de una curiosa pregunta planteada a principios del siglo XVIII en la ciudad rusa de Kaliningrado (entonces llamada Königsberg). El problema de los puentes de Königsberg se preguntaba si sería posible realizar un paseo andando sin salir de la ciudad, dividida en cuatro regiones por el río Pregolia, de modo que se recorriese una sola vez cada uno de los siete puentes que las conectaban.
Este problema llama la atención del genial matemático Leonhard Euler, que estaba de visita en la ciudad, quien demuestra en 1736 que tal paseo es imposible de realizar. Esta demostración está considerada la cuna de la Teoría de Grafos. En ella, Euler conjuga tres grandes técnicas demostrativas.
Primero, sintetiza al máximo la situación, reduciendo cada una de las cuatro regiones del mapa de la ciudad a un punto y cada uno de los siete puentes a una línea, obteniendo lo que hoy se conoce como grafo dual del mapa, consistente en cuatro puntos unidos por siete líneas, como muestra la figura. De este modo, el problema original equivale a dibujar este grafo con un solo trazo, sin levantar el lápiz y recorriendo cada línea una sola vez.
Segundo, Euler emplea un antiguo pero potentísimo método de demostración llamado reducción al absurdo. Euler sabe que habrá demostrado la imposibilidad del paseo si, razonando a partir de la suposición de que tal paseo existiera, alcanza una contradicción flagrante, un absurdo.
Finalmente, para alcanzar esa contradicción, Euler aplica un criterio de paridad. El grafo tiene cuatro vértices. Como solo puede haber un vértice de salida y uno de llegada, los otros vértices tienen que ser vértices de tránsito, es decir, ni se empieza ni se acaba en ellos. Pero eso es imposible, ya que todo vértice de tránsito tendría que tener un número PAR de aristas (la mitad de ellas para llegar al vértice y la otra mitad para salir de él), y todos los vértices del grafo tienen grado impar (3 o 5). Así que… ¡el paseo buscado no puede existir! Los ciudadanos de Königsberg que lo intentaran estaban condenados de antemano al fracaso.
Pulsa aquí para intentar cruzar todos los puentes
Figuras de un solo trazo
Este criterio de paridad es clave para reconocer fácilmente cuándo un grafo se puede dibujar de un solo trazo: o bien todos los vértices tienen grado par (en cuyo caso cualquier vértice servirá de salida y llegada) o bien solo hay dos vértices de grado impar (uno de salida y otro de llegada). En honor a Euler, este recorrido de un solo trazo, de existir, se conoce como camino euleriano.
Pulsa aquí para intentar dibujar de un solo trazo esta figura de un sobre
Grafos simples
Aunque el grafo más famoso corresponde a los puentes de Königsberg, no es lo que hoy conocemos como un grafo simple. Llamamos grafo simple (o sencillamente «grafo», según el contexto) a aquel en donde cada par de vértices no está unido por más de una arista (comprueba que esto no ocurre en el grafo en los puentes de Königsberg, pero sí ocurre en el caso del sobre). A los grafos que no son simples, como el de los puentes, a veces se les denomina multigrafos.
Lema del apretón de manos
Emulando a Euler, ¿serías capaz de deducir el resultado conocido como Lema del apretón de manos?: “En cualquier reunión, el número de personas que estrecha la mano a un número impar de personas es siempre un número par.” (Es decir, el número de vértices de grado impar es siempre par.)
Regiones de proximidad
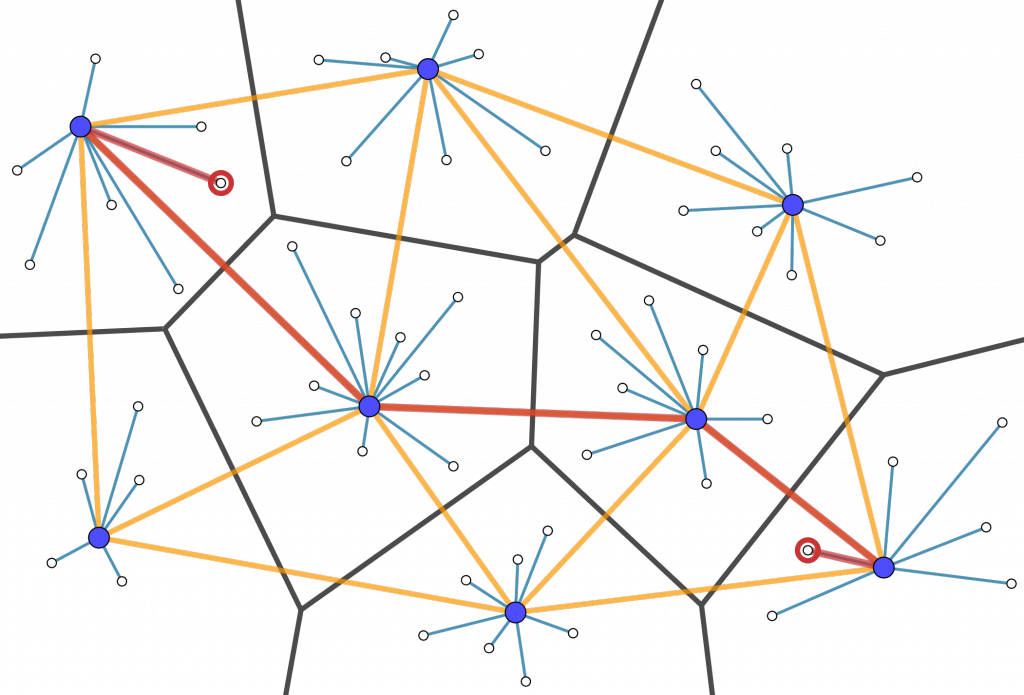
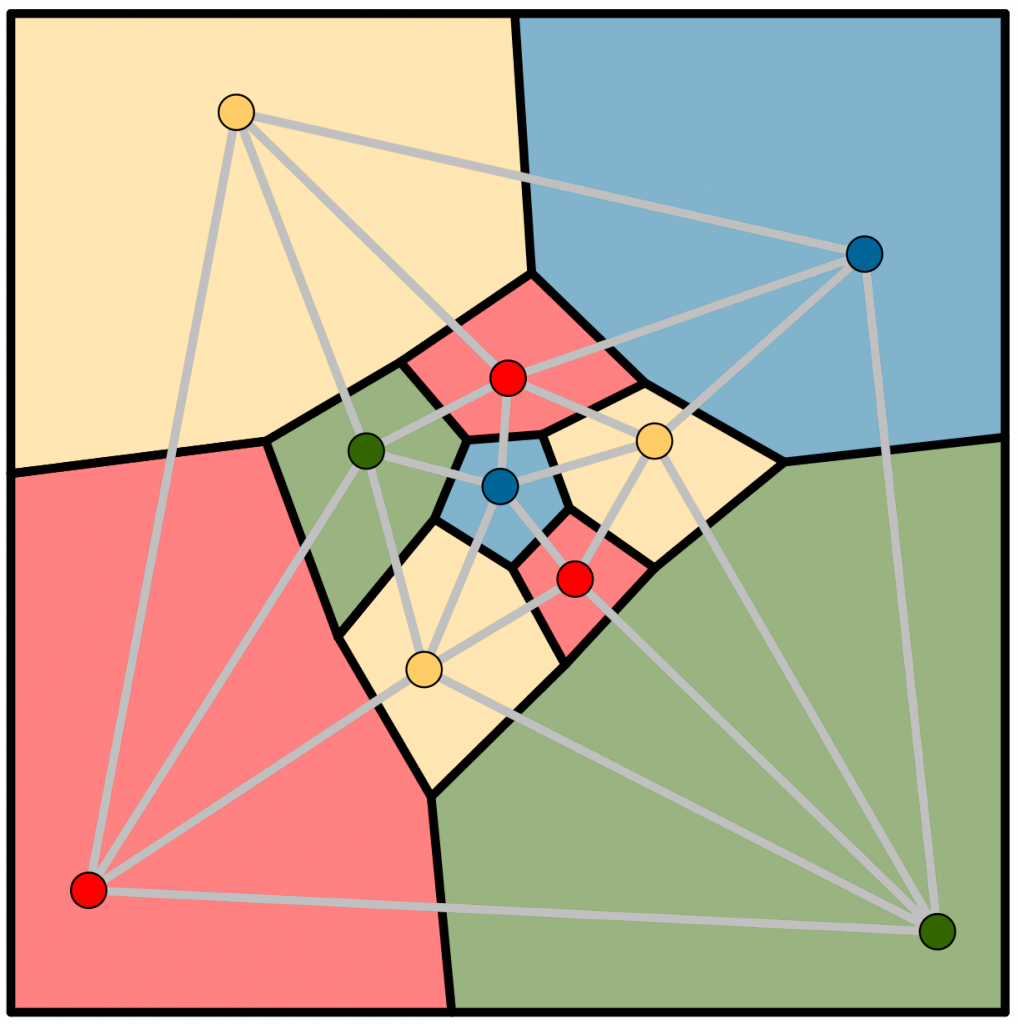
La solución de Euler al problema de los puentes de Königsberg asocia un grafo a un mapa de regiones. En el siglo XIX surgen también problemas recíprocos, que parten de un conjunto de nodos y preguntan acerca de las regiones que deben corresponder a cierto criterio.

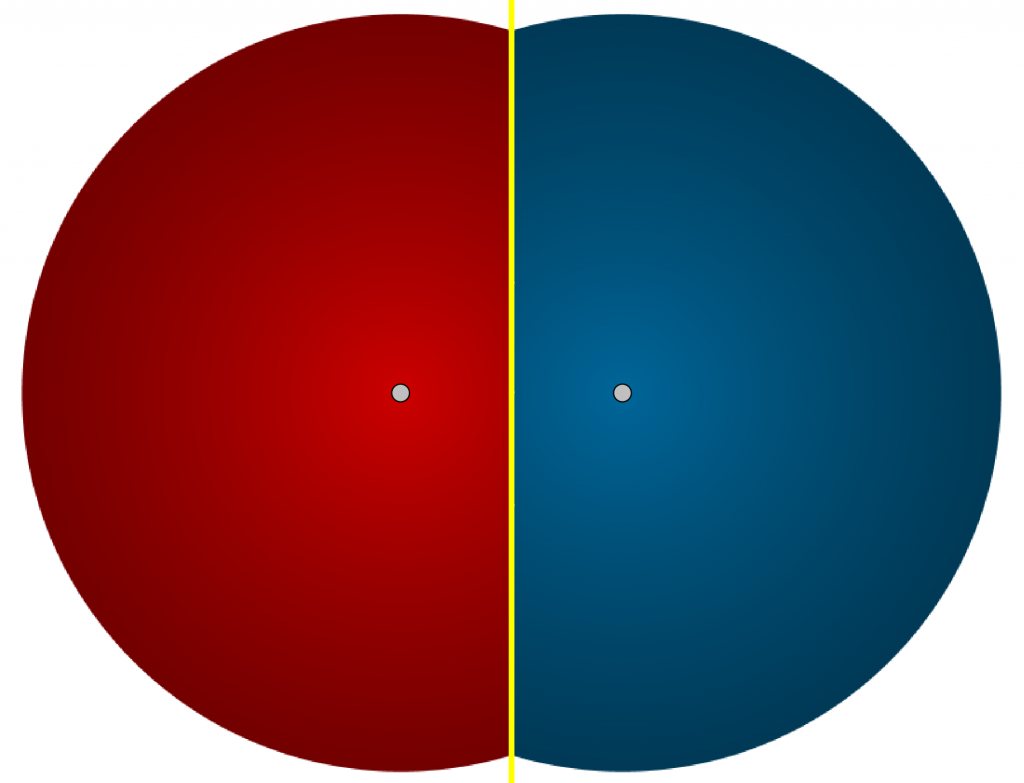
Por ejemplo, dado un conjunto de nodos, ¿cuáles son las regiones formadas por todos los puntos más próximos a cada uno de ellos? La respuesta la da el diagrama de Voronoi correspondiente a esos nodos. Se trata de una división en regiones poligonales (polígonos de Thiessen) cuyos lados descansan sobre algunas mediatrices de los segmentos que unen los nodos.
Podemos generar dinámicamente un diagrama de Voronoi contrayendo simultáneamente circun-ferencias de diferentes colores pero del mismo radio con centro en cada nodo. El rastro de color de cada circunferencia solo sobrevivirá en la región más próxima a cada nodo.
Pulsa aquí para ver cómo se genera dinámicamente una mediatriz
Pulsa aquí para ver cómo se genera dinámicamente un diagrama de Voronoi
Coloración de grafos
Pero es sobre todo una pregunta de coloreado de mapas la que impulsa definitivamente el desarrollo del estudio de los grafos. Esta pregunta, formulada en 1852 por un matemático inglés cuando aún era estudiante es: ¿será posible colorear cualquier mapa plano de regiones utilizando solo cuatro colores, de modo que no haya dos regiones vecinas del mismo color?
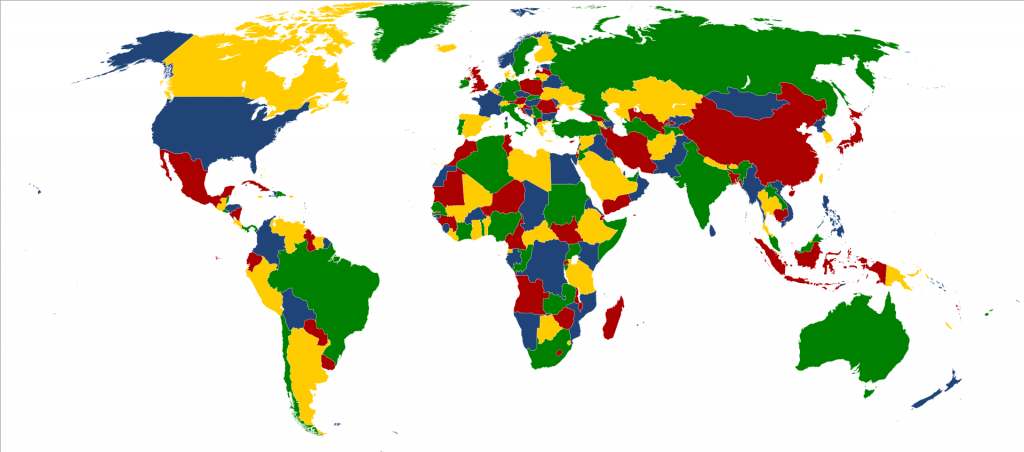
La respuesta, afirmativa, se conoce como teorema de los cuatro colores, pero se tardó más de un siglo en poder demostrarlo. Por fin, en 1970 se obtiene la demostración. Aun así, si bien el resultado es aceptado por la comunidad matemática, la demostración invita a la polémica pues hace uso de un complejo programa de ordenador cuyos resultados no son verificables manualmente. ¿Surgirá algún día otro genio que consiga realizar una “elegante demostración más humana” de este teorema, al estilo de Euler?
Redes y grafos
Piensa en la red de carreteras de España. Son miles de caminos que conectan poblaciones y lugares. La red eléctrica también, solo que los enlaces son ahora cables en vez de carreteras.
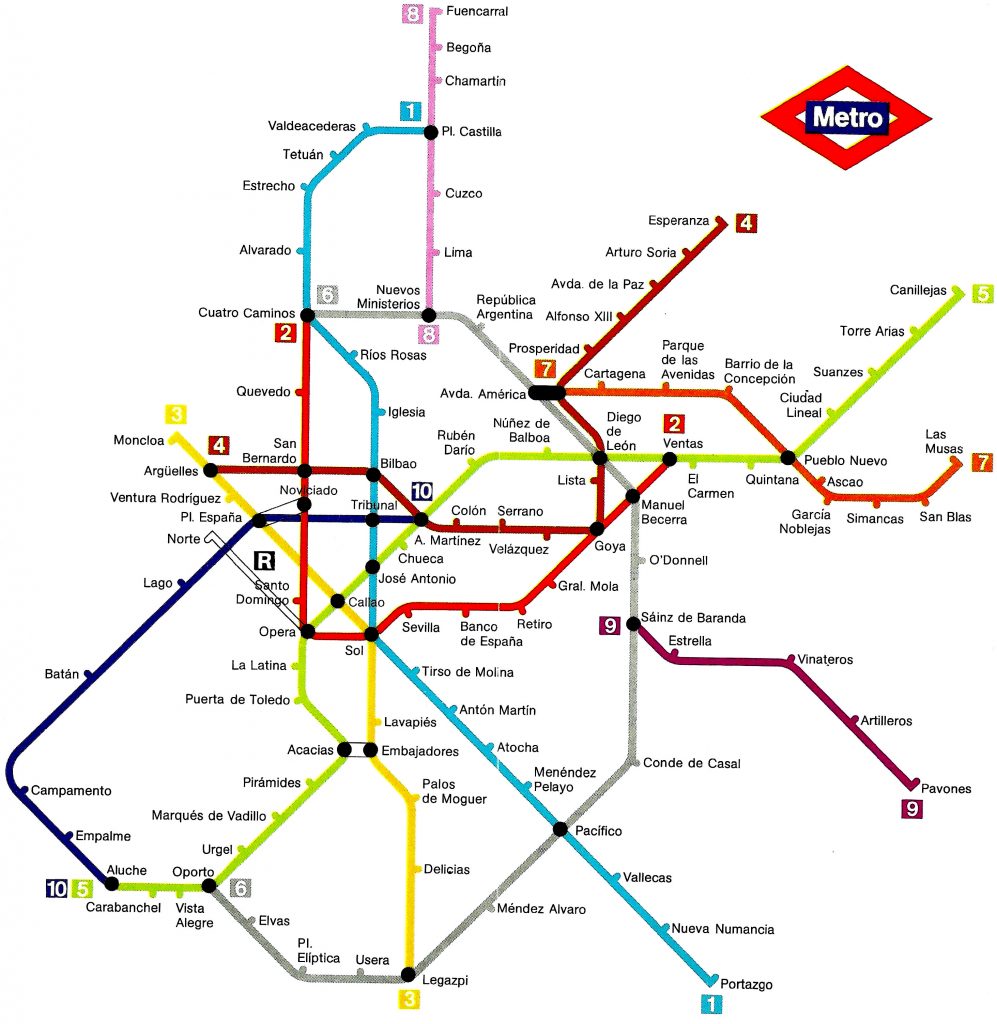
Análogamente, podemos pensar en la redes de autobuses o trenes, la red de metro de una ciudad (el de la figura corresponde a Madrid, año 1982), los circuitos eléctricos y electrónicos, las redes de fibra óptica e inalámbricas, las redes de suministro, las redes sociales, Internet (net significa red), la red de enlaces de los átomos en una molécula, etc.
Nuestro propio cerebro alberga una red neuronal gracias a la cual podemos recordar, imaginar, pensar y sentir. En la actualidad existe ya toda una Ciencia de Redes y muchas herramientas que facilitan la creación y visualización de grafos.
Los grafos tienden a expandirse de modo exponencial. A modo de ejemplo, en el siguiente enlace puedes visualizar el crecimiento del grafo correspondiente a contenidos de GeoGebra en unos siete años.
Pulsa aquí para ver siete años de evolución de GeoGebra
Árboles
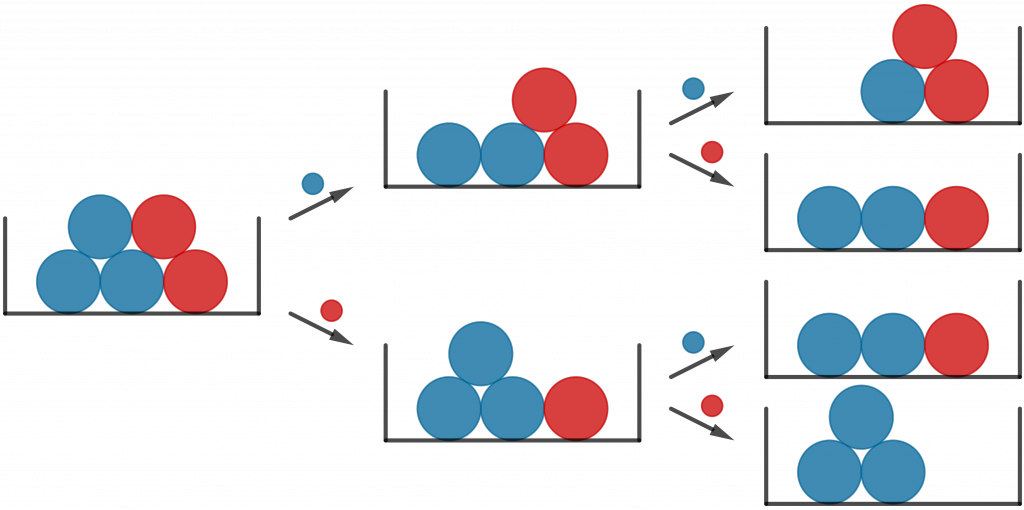
Los grafos son esquemas de redes, que ayudan a analizarlas, independientemente de la naturaleza de los objetos conectados y sus conexiones. Algunos tienen estructura de árbol (solo hay un camino entre cada par de vértices), como los árboles genealógicos y los árboles de probabilidad (ver figura).
Aplicaciones de los grafos
Los grafos se usan en prácticamente todo el mundo tecnológico actual. Gracias a ellos podemos, entre otras aplicaciones:
-
-
-
-
-
- Averiguar rápidamente cuál es el recorrido más corto (en distancia, tiempo o coste) por carretera entre dos lugares (problema del camino más corto, planificador de rutas, algoritmo de Dijkstra)
-
-
-
-
-
-
-
-
-
- Encontrar las mejores escalas para realizar un vuelo (multigrafos)
-
-
-
-
-
-
-
-
-
- Optimizar la distribución de suministros o mensajería (logística)
-
-
-
-
-
-
-
-
-
- Analizar cadenas de amistades en las redes sociales (sociogramas, grados de separación)
-
-
-
-
-
-
-
-
-
- Distinguir o separar claramente zonas o sustancias (coloración de grafos)
-
-
-
-
-
-
-
-
-
- Estudiar la planificación de proyectos (PERT)
-
-
-
-
-
-
-
-
-
- Analizar transiciones de estado (autómatas finitos)
-
-
-
-
-
-
-
-
-
- Ayudar al reconocimiento de imágenes en la visión artificial (segmentación)
-
-
-
-
-
-
-
-
-
- Mejorar la velocidad de búsqueda de información (grafos de conocimiento)
-
-
-
-
-
-
-
-
- Ayudar al rastreo de contagios (modelos epidemiológicos)
-
-
-
Pulsa aquí para ver algunos problemas básicos
Nodos de telefonía fija
Veamos un ejemplo simplificado. Si los vértices representan nodos de telefonía fija, el diagrama de Voronoi correspondiente nos informa de dónde están los usuarios más próximos a cada nodo. Si ahora formamos el grafo dual del diagrama de Voronoi (grafo conocido como triangulación de Delaunay), ya tenemos la ruta que debe seguir una llamada: el usuario que llama se conecta al nodo correspondiente a su región en la teselación de Voronoi, que a su vez conecta con el nodo más próximo al usuario destinatario siguiendo el camino más corto en el grafo de Delaunay; finalmente, desde este nodo se comunica con el usuario destinatario de la llamada.
Pulsa aquí para ver este proceso
Número cromático
La coloración de grafos permite visualizar y analizar diferentes relaciones entre vértices conectados de un grafo. Por ejemplo, imagina que en una fiesta coinciden seis personas. Cada par de personas (hay 15 parejas posibles), o bien ya se conocen o bien son mutuamente desconocidas. Pues bien, un resultado conocido como Teorema de amigos y extraños, muy fácil de demostrar coloreando grafos, dice: “En cualquier grupo de seis personas, hay tres de ellas mutuamente conocidas o mutuamente desconocidas.”
En la siguiente aplicación puedes intentar colorear pequeños mapas con el mínimo de colores posible (número cromático). Recuerda que dos regiones vecinas no pueden tener el mismo color. Esto equivale a colorear los vértices del grafo dual de modo que se diferencien los colores de cualquier par de vértices extremos de la misma arista.
Pulsa aquí para colorear pequeños mapas
Pulsa aquí si te atreves con un reto mayor
Five Room Puzzle
Five Room es uno de los más antiguos rompecabezas relacionados con los grafos, descrito en 1957 por Martin Gardner.
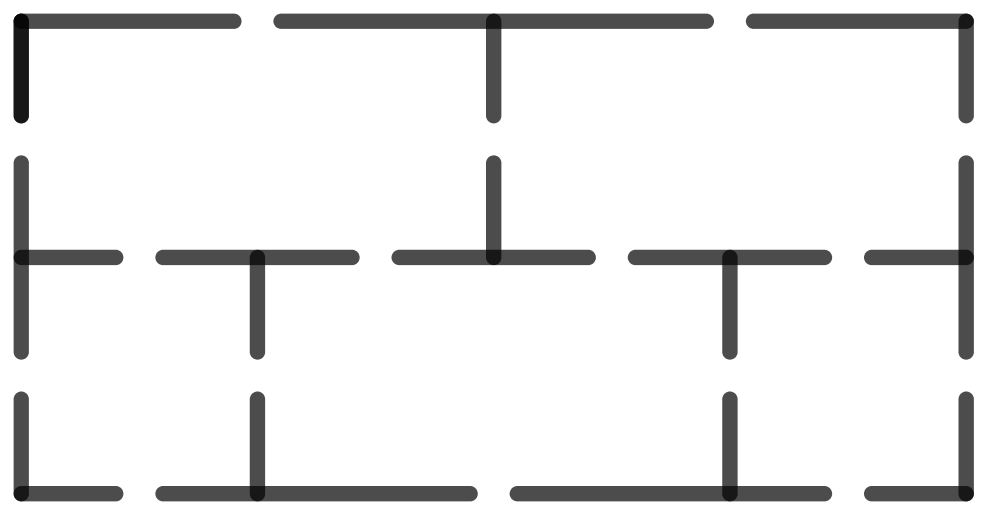
Casa de 16 puertas

Casa de 15 puertas
Observa el croquis de una casa de cinco espacios con 16 puertas. Es imposible realizar un paseo que pase una sola vez por cada una de las 16 puertas. ¿Sabrías demostrarlo? Pero en la versión con 15 puertas, sí es posible: ¡encuéntralo!
Pulsa aquí para intentar resolver el puzzle
Isomorfismos de grafos
Observa que la forma de la figura del puzzle es irrelevante. Tal y como pensó Euler en el problema de los puentes, lo importante es su grafo dual. Y en este, el número de vértices y el número de aristas que concurren en cada uno de ellos.
Cuando dos grafos son equivalentes porque tienen el mismo número de vértices y cada arista de uno corresponde a una arista del otro, se dice que son isomorfos.
Grafos planos
Por razones de estética y claridad, es habitual transformar, si es posible, un grafo en otro isomorfo sin aristas que se corten. Cuando puede conseguirse, se dice que el grafo es plano.
En la siguiente aplicación puedes ver una transformación continua entre grafos isomorfos correspondientes al puzzle anterior. El último grafo, sin cortes de aristas, muestra que el grafo es plano.
Pulsa aquí para ver la transformación
Esqueletos de los poliedros
Observa que, en el ejemplo anterior, el grafo correspondiente al puzzle no es un grafo simple.
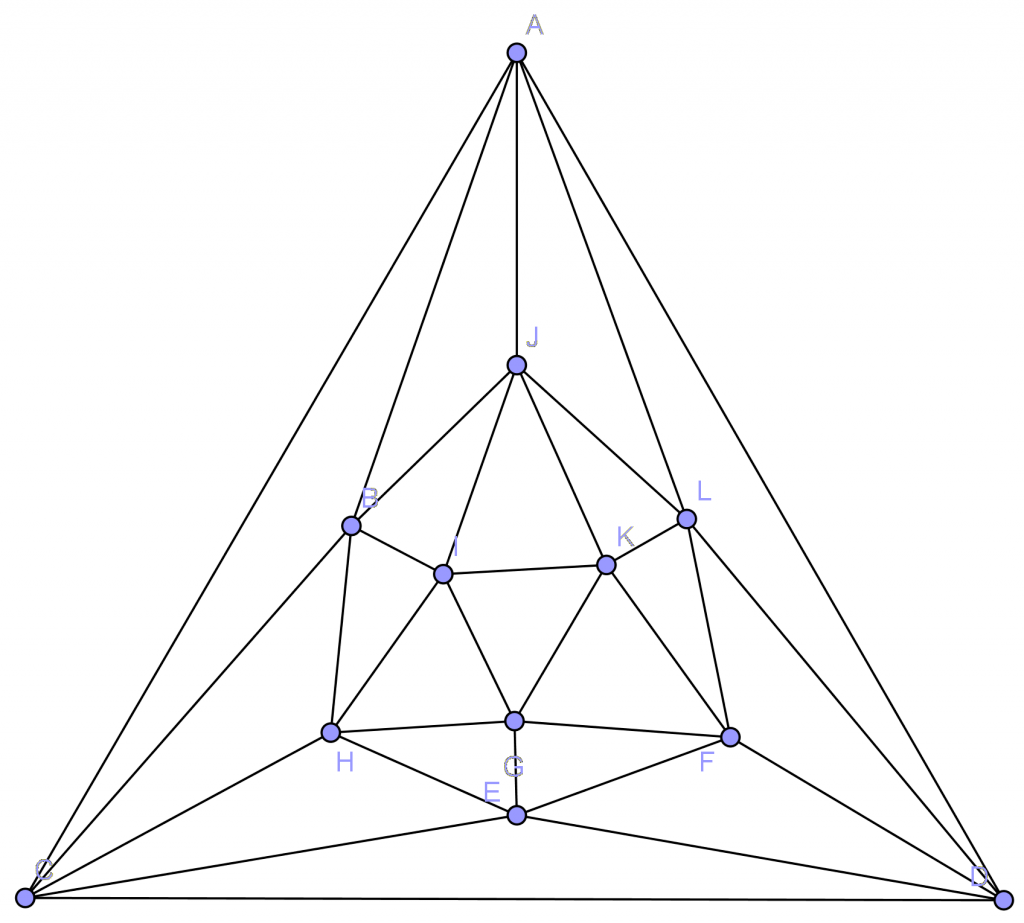
Por el contrario, si proyectamos las aristas de cualquier poliedro sobre un plano, el grafo resultante es siempre un grafo simple. Esto es evidente, ya que dos vértices de un poliedro nunca se unen por más de una arista.
Pues bien, se puede demostrar que este grafo resultante siempre es un grafo plano, es decir, podemos transformarlo en un grafo isomorfo en donde ningún par de aristas se corte (diagrama de Schlegel).
En la siguiente aplicación, intenta transformar el grafo simple, resultado de proyectar un icosaedro, en un grafo plano (es decir, intenta que las aristas no se corten). Para ello, en la aplicación, activa la casilla Grafo y aplica este método: elige una región y coloca el resto de los vértices dentro.
Caminos hamiltonianos
Hacia 1850 el matemático W. R. Hamilton patentó un juego que llamó Viaje por el Mundo. Consistía en encontrar un recorrido que pasase por 20 ciudades situadas en los nodos del grafo del dodecaedro (que es equivalente a un recorrido por los 20 vértices del dodecaedro). Desde entonces, se llaman caminos hamiltonianos a los recorridos que visitan todos los vértices de un grafo una sola vez (en los caminos eulerianos, era cada arista la que se recorría una sola vez).
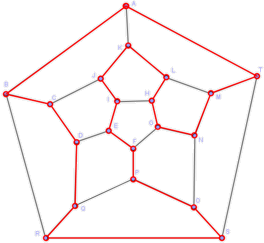
Puedes intentar encontrar un camino hamiltoniano en el icosaedro de la aplicación anterior. También puedes intentar resolver el juego original de Hamilton usando esa aplicación (elige dodecaedro en vez de icosaedro). En ambos casos, si activas la casilla «Cadena» podrás ayudarte de la cadena roja para señalar el recorrido.
Grafos completos
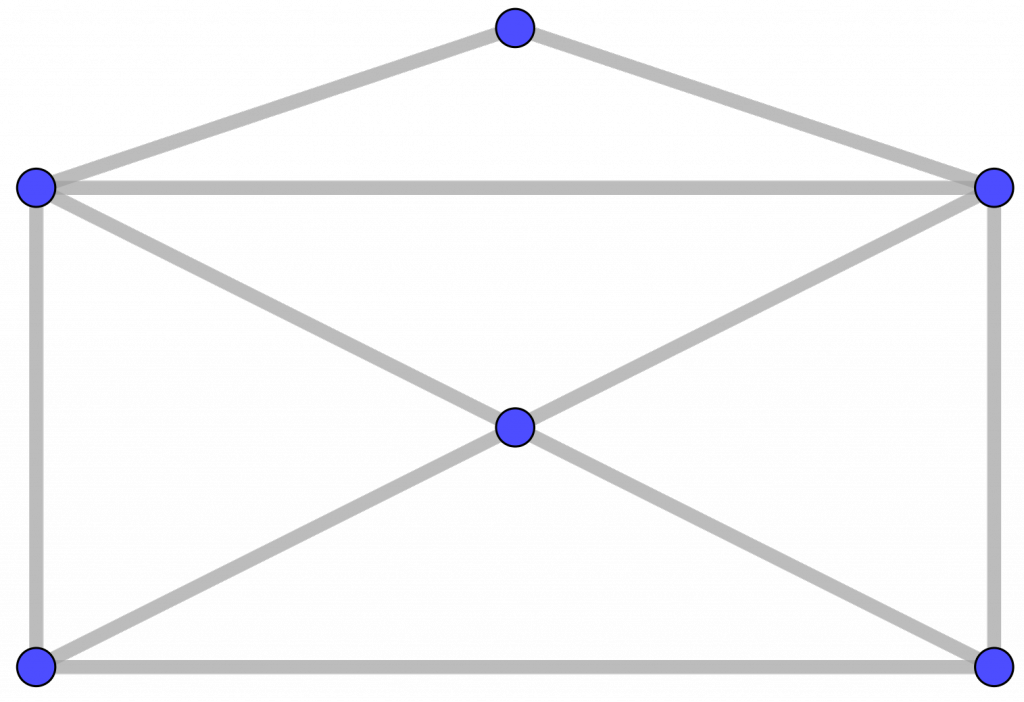
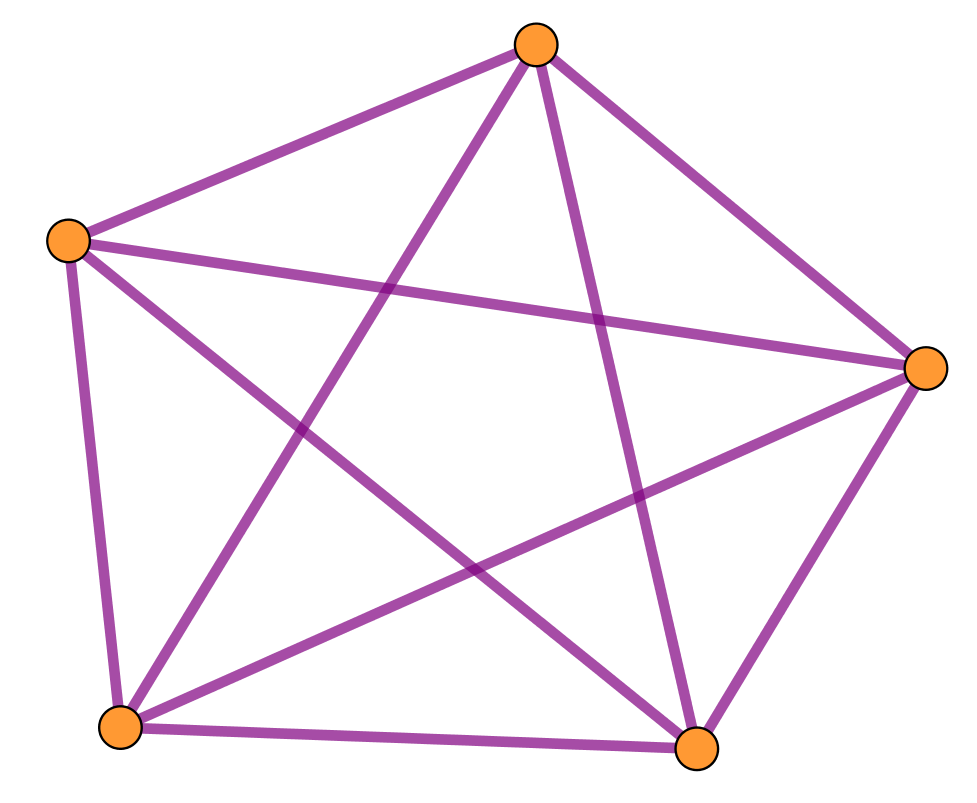
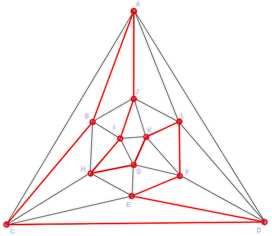
Los grafos simples que unen todos los pares de vértices se llaman grafos completos. Si el número de vértices es n, al grafo completo correspondiente se le denomina Kn. Cada uno de ellos es isomorfo a un polígono regular de n vértices con todas sus diagonales.
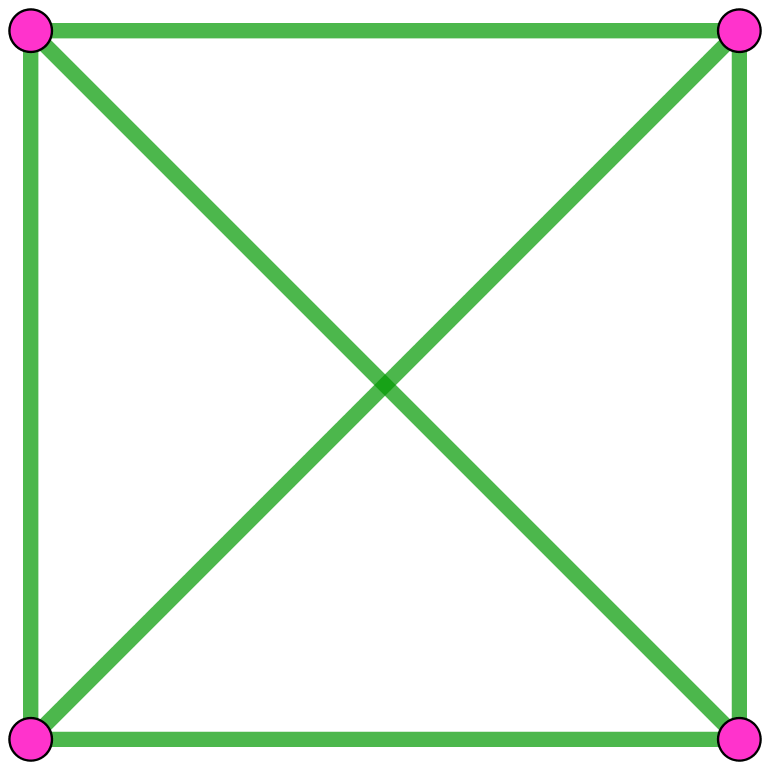 ¿Puedes calcular cuántas aristas tiene un grafo completo de n vértices?
¿Puedes calcular cuántas aristas tiene un grafo completo de n vértices?
Por ejemplo, K4 tiene 6 aristas (ver figura). ¿Y K5? ¿Y K6? ¿Puedes encontrar la fórmula general?
En la siguiente aplicación puedes ver algunos de estos grafos. Además, la aplicación puede ayudarte a razonar cuál es el número de aristas que debe tener un grafo completo de n vértices.
Pulsa aquí para ver algunos grafos completos
Ningún grafo completo con más de 5 vértices puede ser plano, porque todos contienen a K5 y este no es plano, como puedes comprobar en la siguiente aplicación (teorema de Kuratowski).
Pulsa aquí para comprobar que K5 no es un grafo plano
Grafos bipartitos completos
En un grafo completo, todo vértice se conecta a todos los demás. Si previamente dividimos los vértices en dos grupos (como si estuviesen enfrentados), podemos pensar en el grafo que conecta cada vértice de un grupo con todos los vértices del otro grupo. Un grafo así se denomina bipartito completo.
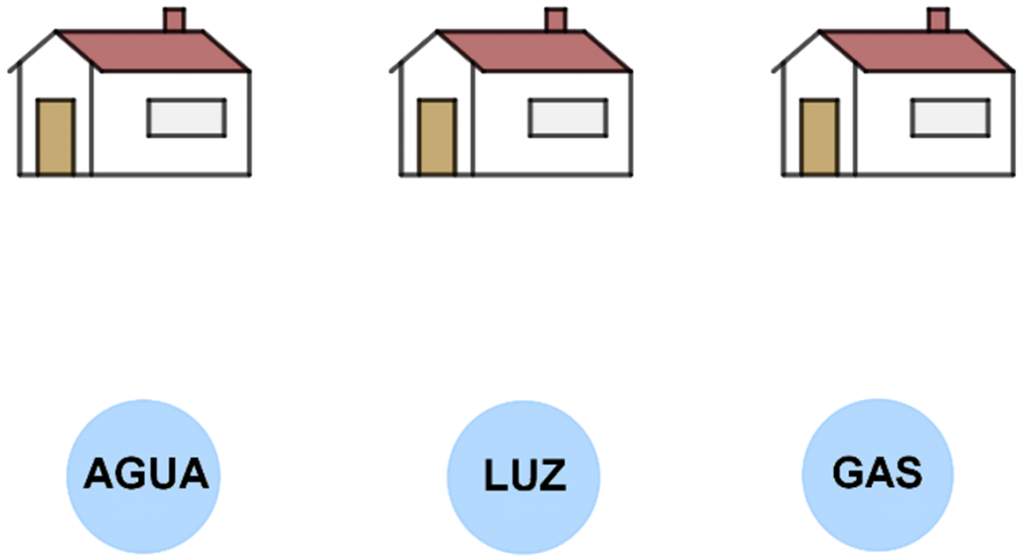 Un ejemplo muy conocido de este tipo de grafos es el que plantea el famoso problema de las tres casas y los tres servicios (K3,3). Se trata de conectar tres casas con tres fuentes de suministros (agua, luz y gas), sin que las conexiones se entrecrucen. En la ampliación de la actividad 4 del cuadernillo de actividades verás un razonamiento que demuestra que tal grafo no es posible en el plano, pero sí en otras superficies (puedes intentarlo en las hojas de ejercicios).
Un ejemplo muy conocido de este tipo de grafos es el que plantea el famoso problema de las tres casas y los tres servicios (K3,3). Se trata de conectar tres casas con tres fuentes de suministros (agua, luz y gas), sin que las conexiones se entrecrucen. En la ampliación de la actividad 4 del cuadernillo de actividades verás un razonamiento que demuestra que tal grafo no es posible en el plano, pero sí en otras superficies (puedes intentarlo en las hojas de ejercicios).
En el apartado anterior, tal vez hayas llegado a la conclusión correcta de que un grafo completo de n vértices (Kn) tiene siempre n(n-1)/2 aristas. ¿Sabrías ahora averiguar cuántas aristas tiene un grafo bipartito completo Kn,m de «n» vértices de un grupo conectados con todos los «m» vértices de otro grupo? Por ejemplo, K3,3 tiene 9 aristas.
Matriz de adyacencia
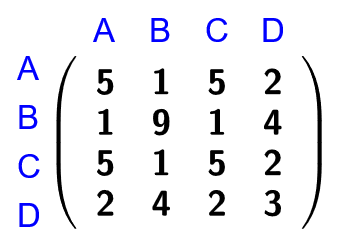
La información recogida en un grafo también se puede expresar mediante números, lo que facilita los cálculos computacionales en grandes redes. Por ejemplo, la información del grafo de los puentes de Königsberg puede recogerse en una matriz, llamada matriz de adyacencia.
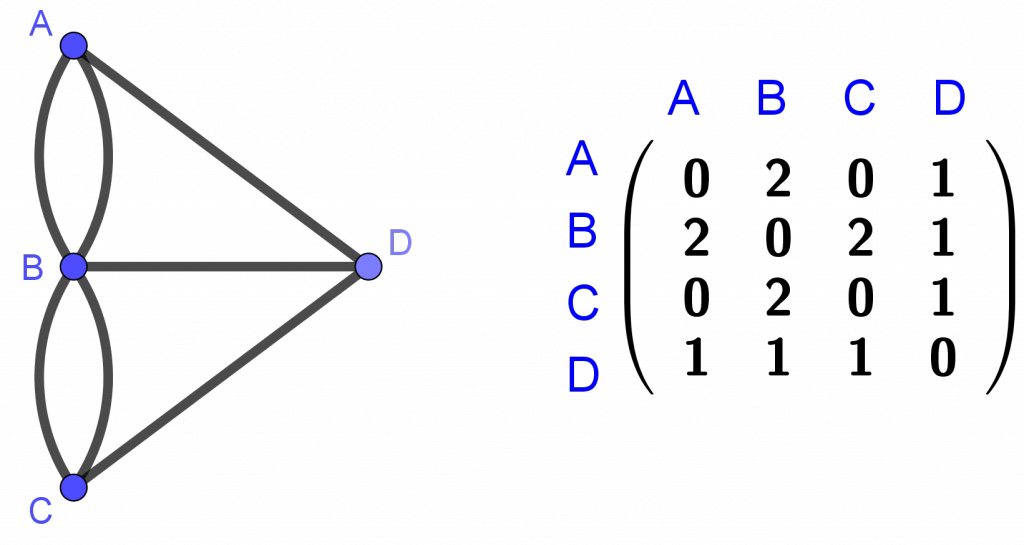 Cada fila de la matriz representa el número de aristas que comparte un vértice con cada uno de los vértices. La suma de todos los números de una fila es el grado del vértice correspondiente.
Cada fila de la matriz representa el número de aristas que comparte un vértice con cada uno de los vértices. La suma de todos los números de una fila es el grado del vértice correspondiente.
Nota: Observa que la matriz es simétrica, ya que si una arista conecta A con B, también conecta B con A. Sin embargo, hay grafos (llamados grafos dirigidos) en donde cada arista tiene una orientación, de modo que A puede conectar con B pero no al revés. En ese caso, la matriz de adyacencia no será simétrica.
Número de caminos entre dos nodos
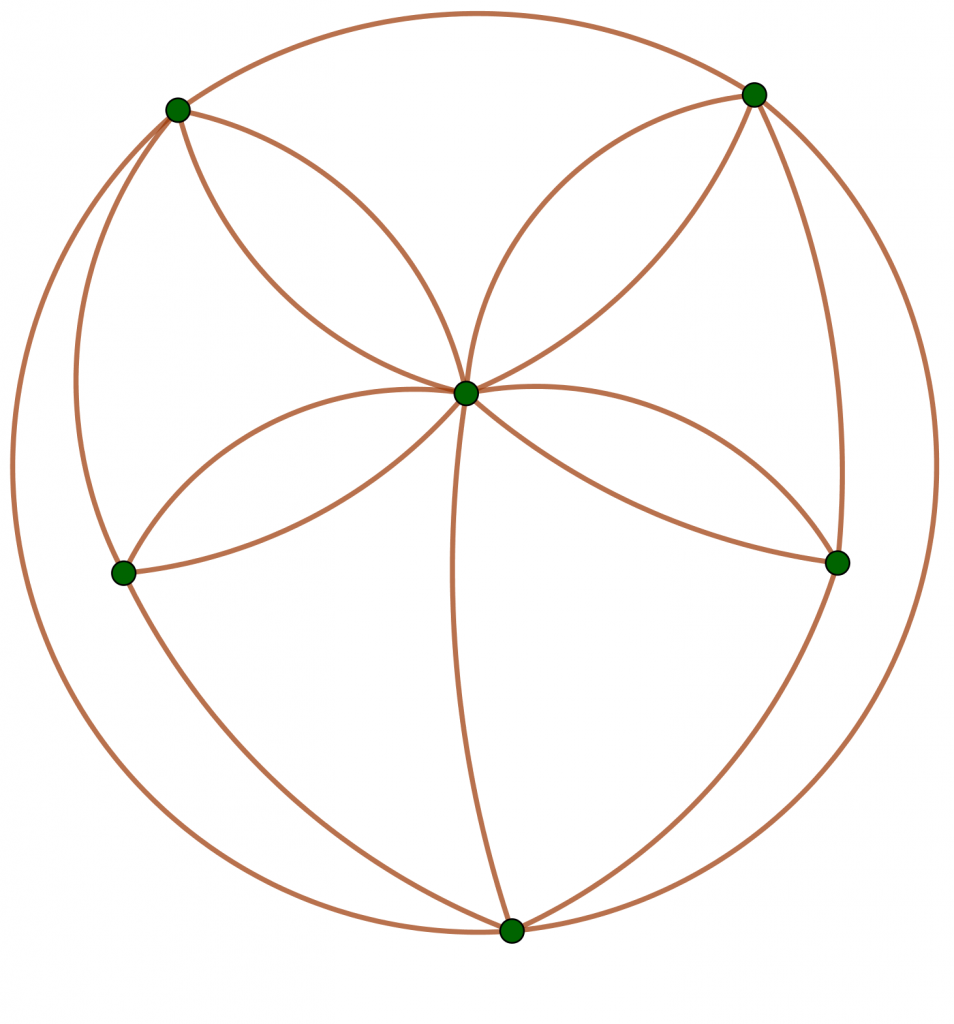
Imagina un árbol en el que el tronco se divide en dos ramas, cada rama en otras dos, y así sucesivamente. El número de ramas, cada vez más alejadas del tronco, va creciendo de forma exponencial. El número de cada tipo de ramas es fácil de calcular, ya que ha de ser una potencia de dos: 20 (un tronco), 21 (dos ramas principales), 22 (cuatro ramas secundarias), 23 (ocho ramas terciarias), etc.
Ya hemos visto que la estructura de un árbol es un caso particular de grafo. ¿Existe algún modo de contar rápidamente el número de caminos entre dos nodos de un grafo que no tenga estructura de árbol? Pues sí, existe, gracias a la matriz de adyacencia.
Del mismo modo que el número de ramas de un árbol que se bifurca sigue una sucesión de potencias de 2, el número de caminos de un grafo cualquiera sigue una sucesión de potencias de su matriz de adyacencia M: M0, M1, M2, M3, etc.
En la siguiente aplicación partimos del grafo correspondiente a los puentes de Königsberg y de su matriz de adyacencia M. Al multiplicar sucesivamente M por sí misma (es decir, al calcular las sucesivas potencias), obtenemos el número de caminos para ir de un nodo a otro.
Por ejemplo, el primer elemento de la siguiente matriz, que es M2, indica que hay 5 caminos diferentes para salir de A, cruzar 2 puentes (que pueden ser el mismo) y volver a A. Observa, en la aplicación, que incluso se cumple para el caso de exponente 0.
Pulsa aquí para ver el cálculo del número de caminos de un grafo
Actividades
Bibliografía
Teoría de grafos
-
-
-
-
- ALSINA, Claudi: Mapas del metro y redes neuronales: La Teoría de Grafos. Editorial RBA. Barcelona, 2017. Colección National Geographic, nº 11.
- DURÁN, Guillermo: Teoría de Grafos . FCEyN, UBA/CONICET. Montevideo, 2008.
-
-
-
Matemática recreativa con grafos
-
-
-
-
- BOLT, Brian: Divertimentos matemáticos. Editorial Labor. Barcelona, 1988.
- BOLT, Brian: Más actividades matemáticas. Editorial Labor. Barcelona, 1988.
- CORIAT, M./SANCHO, J.M./GONZALVO, P./MARÍN, A.: Nudos y nexos. Redes en la escuela. Editorial Síntesis. Madrid, 1989. Colección Matemáticas: cultura y aprendizaje.
- DUDENEY, HENRY E.: El Acertijo del Mandarín y otras diversiones matemáticas. Editorial Zugarto. Madrid, 1992.
- GARDNER, Martin: Juegos y enigmas de otros mundos. Editorial Gedisa. Barcelona, 1987.
- GARDNER, Martin: Mosaicos de Penrose y escotillas cifradas. Editorial Labor. Barcelona, 1990.
- GARDNER, Martin: Rosquillas anudadas: Editorial Labor. Barcelona, 1985.
- GARDNER, Martin: Ruedas, Vida y otras diversiones matemáticas. Editorial Labor. Barcelona, 1987.
- GUZMÁN, Miguel de: Cuentos con cuentas. Editorial Labor. Barcelona, 1987. Tercera edición.
- HOLT, Michael: Matemáticas recreativas 2. Editorial Martínez Roca. Barcelona, 1986.
- HOLT, Michael: Matemáticas recreativas 3. Editorial Martínez Roca. Barcelona, 1988.
- LOYD, Sam: Los acertijos de Sam Loyd. Editorial Zugarto. Madrid, 1992.
- MALEY, A./GRELLET, F.: Acertijos de la Universidad de Cambridge. Editorial Selector. México D.F., 1989.
-
-
-
Poliedros y la fórmula de Euler
-
-
-
-
- ALSINA, C./BURGUÉS, C./FORTUNY J.M.: Materiales para construir la geometría. Editorial Síntesis. Madrid, 1991. Colección Matemáticas: cultura y aprendizaje.
- BOLT, Brian: Actividades matemáticas. Editorial Labor. Barcelona, 1988.
- BOLT, Brian: Aún más actividades matemáticas. Editorial Labor. Barcelona, 1989.
- DUNN, Ángela: El concurso de belleza y otros desafíos matemáticos. Editorial Zugarto. Madrid, 1992.
- GARCÍA, J./BERTRÁN, C.: Geometría y experiencias. Editorial Alhambra, 1988.
- GUZMÁN, Miguel de: Cuentos con cuentas. Editorial Labor. Barcelona, 1987. Tercera edición.
-
-
-
El toro
-
-
-
-
- BOLT, Brian: Actividades matemáticas. Editorial Labor. Barcelona, 1988.
- GARDNER, Martin: Viajes por el tiempo y otras perplejidades matemáticas. Editorial Labor. Barcelona, 1988.
- GARDNER, Martin: ¡Ajá! Paradojas. Editorial Labor. Barcelona, 1989. Cuarta edición.
-
-
-
El triángulo de Tartaglia y el binomio de Newton
-
-
-
-
- BOLT, Brian: Actividades matemáticas. Editorial Labor. Barcelona, 1988
-
-
-
Árboles, combinatoria y grafos dirigidos
-
-
-
-
- GARDNER, Martin: El ahorcamiento inesperado y otros entretenimientos matemáticos. Alianza Editorial. Madrid, 1991.
- GARDNER, Martin: Festival mágico-matemático. Alianza Editorial. Madrid, 1984.
- GARDNER, Martin: Inspiración ¡ajá!. Editorial Labor. Barcelona, 1981.
- GARDNER, Martin: Ruedas, Vida y otras diversiones matemáticas. Editorial Labor. Barcelona, 1985.
- GUZMÁN, Miguel de: Aventuras matemáticas. Editorial Labor. Barcelona, 1988.
- GUZMÁN, M./COLERA, J./SALVADOR, A.: Matemáticas 1º BUP. Editorial Anaya. Madrid, 1991.
- MASON, J./BURTON, L./STACEY, K.: Pensar matemáticamente. Editorial Labor. Barcelona 1992.
- SOCAS, M.M./CAMACHO, M./PALAREA, M./HERNÁNDEZ, M.: Iniciación al álgebra. Editorial Síntesis. Madrid, 1989. Colección Matemáticas: cultura y aprendizaje.
-
-
-
Matrices de adyacencia
-
-
-
-
- CORIAT, M./SANCHO, J.M./GONZALVO, P./MARÍN, A.: Nudos y nexos. Redes en la escuela. Editorial Síntesis. Madrid, 1989. Colección Matemáticas: cultura y aprendizaje.
-
-
-
Funciones
-
-
-
-
- AZCÁRATE, C./DEULOFEU, J.: Funciones y gráficas. Editorial Síntesis. Madrid, 1990. Colección Matemáticas: cultura y aprendizaje.
- SHELL CENTRE OF MATHEMATICAL EDUCATION: El lenguaje de funciones y gráficas. MEC (Universidad País Vasco). Bilbao, 1990.
-
-
-
Didáctica
-
-
-
-
- HERNÁN, Francisco: Retrato de una profesión imaginada. Editorial Proyecto Sur. Granada, 1991.
- HERNÁN, F./CARRILLO E.: Recursos en el aula de matemáticas. Editorial Síntesis. Madrid, 1989.
- RESNICK, L.B./FORD, W.W.: La enseñanza de las matemáticas y sus fundamentos psicológicos. MEC. Madrid, 1990.
-
-
-