DESCARGA EL PDF castellano DESCARGA O PDF galego
Autor: Guido Ramellini
Aplicaciones interactivas: Rafael Losada Liste y José Muñoz Santoja
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- Cuadrados latinos
- Cuadrados grecolatinos. CGL
- Reto #1
- Reto #2
- La hipótesis de Euler
- La llegada de los ordenadores
- Los cuadrados Grecolatinos en la literatura
- Los cuadrados Grecolatinos en las artes plásticas: los cuadrados mágico
- Aplicaciones de los cuadrados Grecolatinos
- El diseño experìmental factorial
- Bibliografía
- ¡A jugar! Juegos relacionados con el cuadrado grecolatino
- Maquetas para construir los juegos
El juego y la belleza están en el origen de una gran parte de las matemáticas.
Si los matemáticos de todos los tiempos se lo han pasado tan bien jugando y contemplando su juego y su ciencia, ¿por qué no tratar de aprenderla y comunicarla a través del juego y de la belleza?
Miguel de Guzmán
No dejamos de jugar porque envejecemos; envejecemos porque dejamos de jugar.
B. Shaw
Cuadrados latinos

En los últimos años de su vida, Leonhard Euler (1707-1783) escribió una voluminosa memoria acerca de un tipo de cuadrados mágicos: los cuadrados latinos.
La característica de los cuadrados latinos es que no se repite el mismo símbolo en ninguna de las filas o columnas.
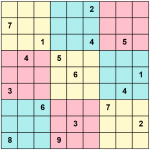
¡Exacto!, como en los Sudokus, que son cuadrados latinos 9×9 especiales, ya que se pueden descomponer en 9 cuadrados diferenciados 3×3.
Cuadrados grecolatinos. CGL

Si juntamos dos cuadrados latinos ortogonales – en los que los elementos homólogos respectivos coinciden una única vez –, usando otros símbolos, para no confundirlos, se consigue un nuevo cuadrado, con las mismas características de los anteriores y en cuyas casillas no se repite nunca la misma combinación de símbolos. Es un cuadrado grecolatino.
En el texto de Euler se contemplan cuadrados grecolatinos en los que se repiten símbolos en las diagonales.
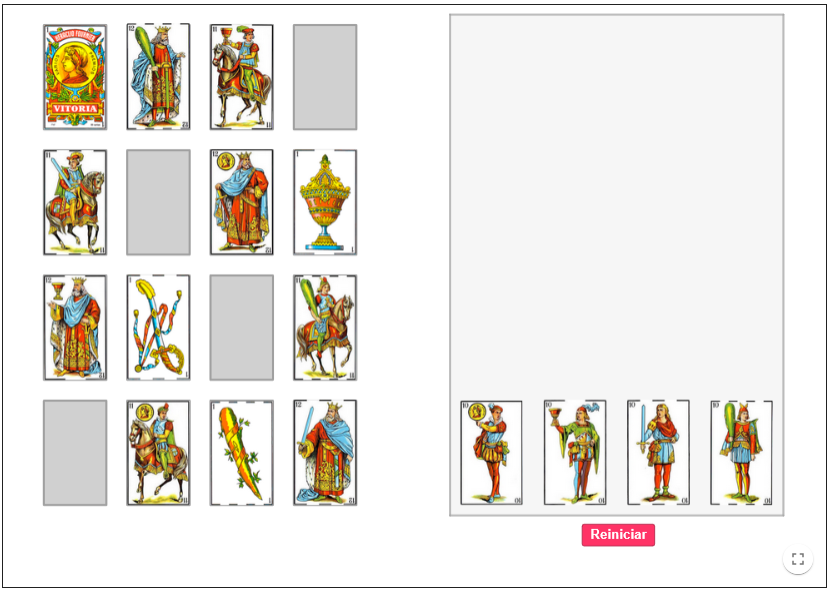
Reto #1
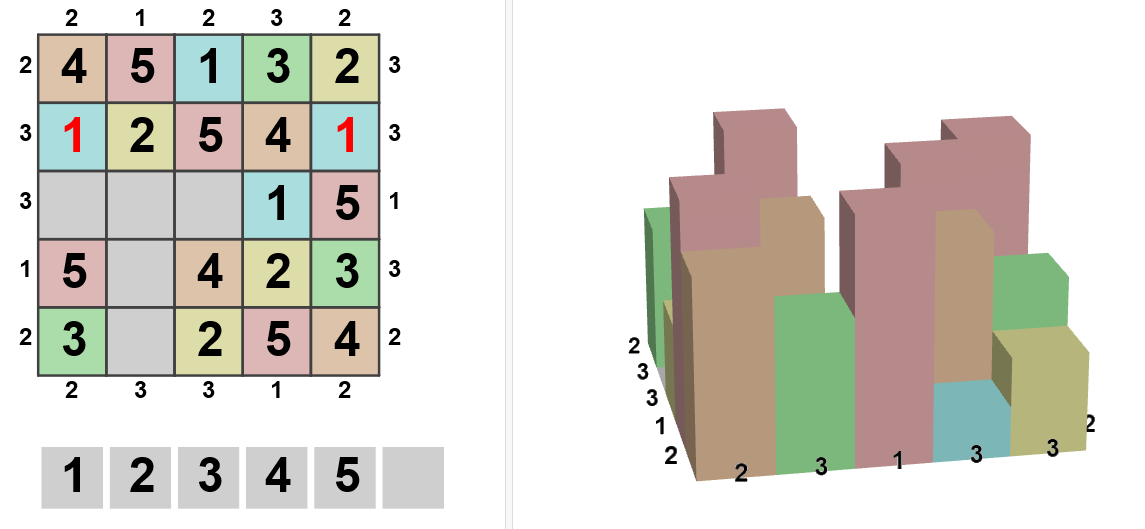
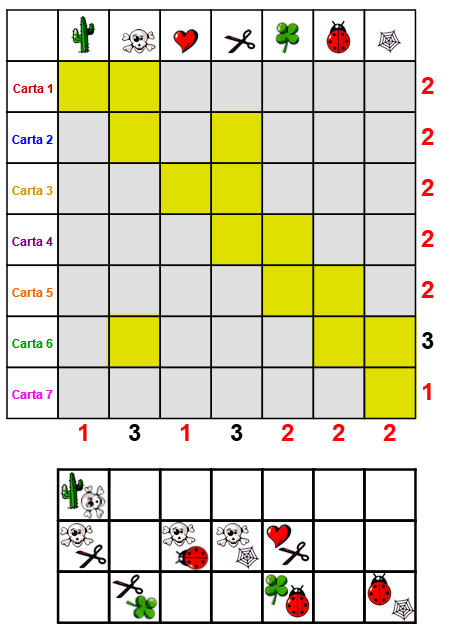
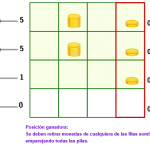
Completa este Cuadrado, introduciendo correctamente estos elementos
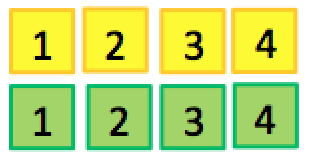
Puedes utilizar esta aplicación
Es fácil comprobar, por ejemplo: usando unos naipes, que:
- No existe solución para los cuadrados 2×2;
- Que repetir los símbolos en las diagonales es condición indispensable para resolver CGL 3×3;
Más difícil es comprobar que no hay solución para los QGL 6×6.
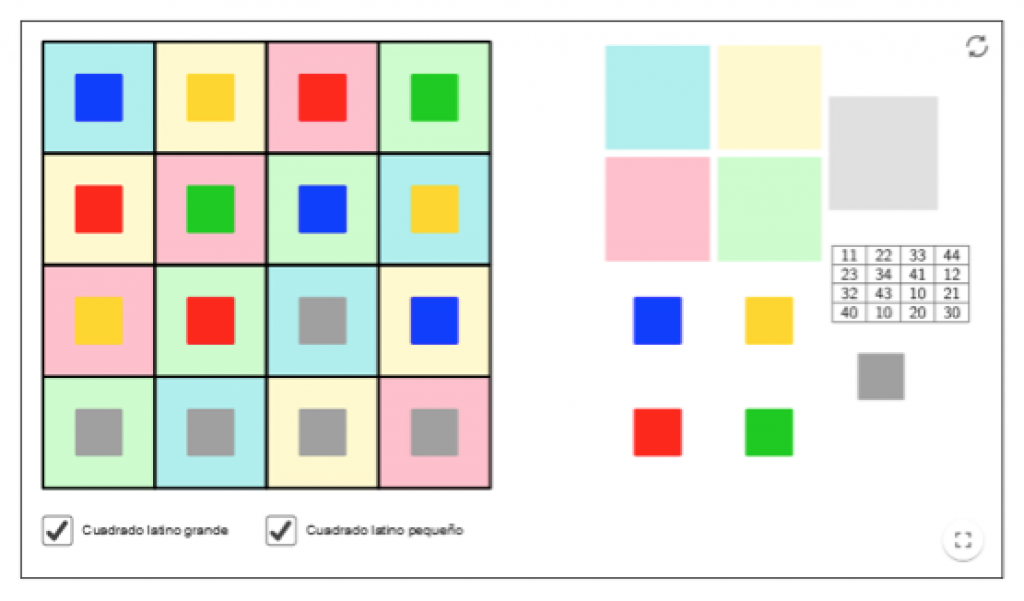
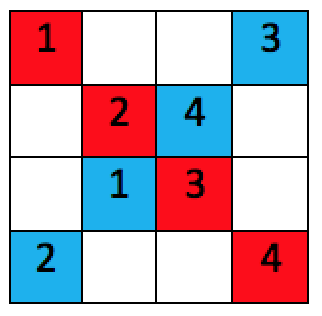
Reto #2
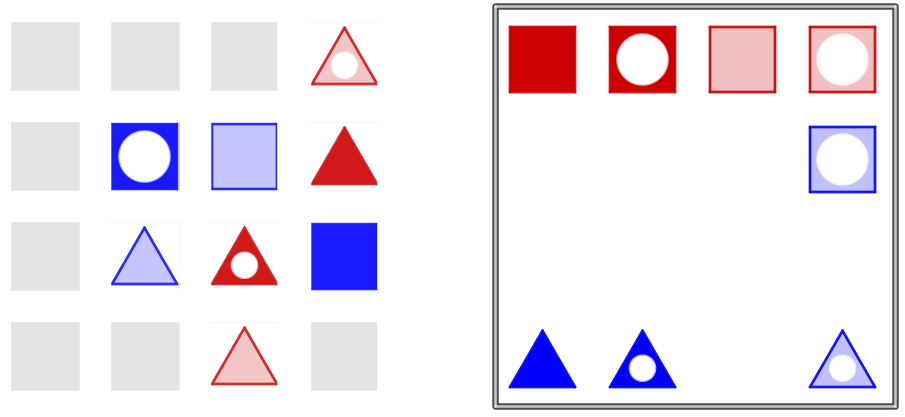
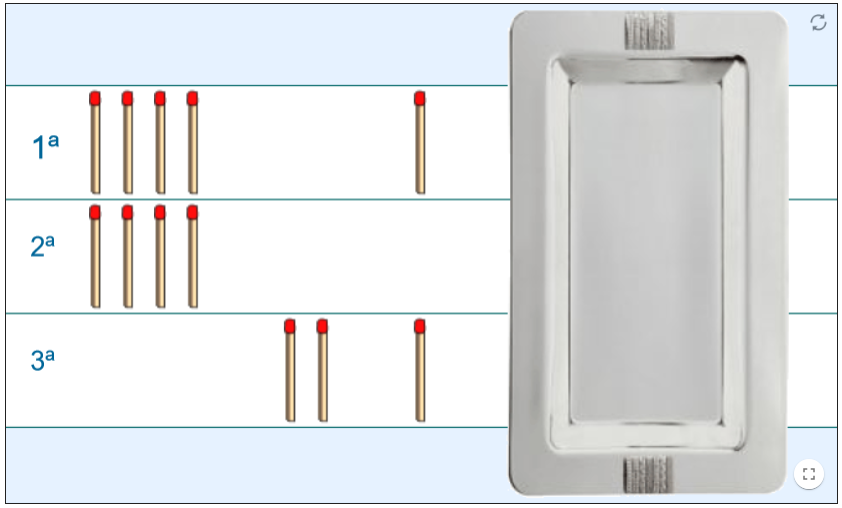
Transformar esta posible solución del Reto #1, que repite el color de las fichas en las diagonales, en un Cuadrado Grecolatino en el que las dos características (color y número) no se repiten tampoco en las diagonales principales.
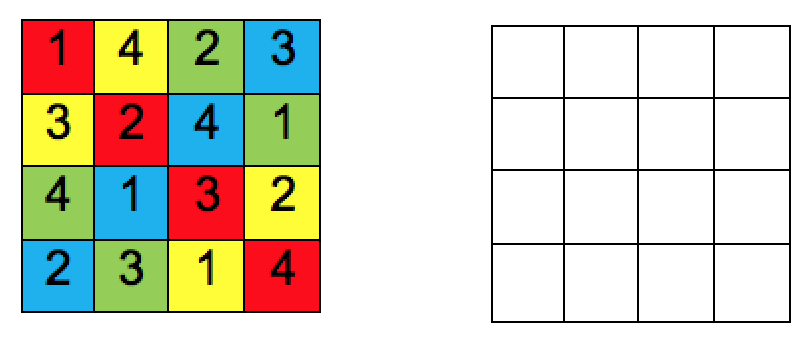
Puedes utilizar la técnica de las permutaciones de filas y columnas que explicamos en el anexo del final.
La hipótesis de Euler
Euler demostró que no hay cuadrados grecolatinos de orden 2; y construyó sin problemas cuadrados de orden 3, 4 y 5. ¿pero qué decir de los cuadrados de orden 6? Euler afrontó el problema imaginando 36 soldados, con 6 distintos grados y de 6 regimientos diferentes.
«Yo no dudo en concluir que es imposible hallar un cuadrado completo de 36 casillas ni en hacer extensiva tal imposibilidad a los casos n=10, n=14 y, en general a todos los órdenes pares de clase impar (no divisibles por 4). Interrumpo aquí mis investigaciones sobre la cuestión, que aunque de escasa utilidad por sí misma, nos ha conducido a importantes observaciones en la teoría combinatoria y en la teoría general de los cuadrados mágicos».
L. Euler

Euler había afrontado el problema imaginando 36 soldados, con 6 distintos grados y de 6 regimientos diferentes. El problema estaba en disponerlo en 6 filas y 6 columnas de manera que en cada una haya un y sólo un soldado con el mismo grado y del mismo regimiento.
En 1901, Gaston Tarry publicó una demostración que, a través de pruebas empíricas, confirmaba la validez de la conjetura de Euler para el orden 6.
Pero Euler se equivocó en parte. En 1959, E. T. Parker, R. C. Bose y S. S. Shrikhande presentaron un método para construir infinitos cuadrados grecolatinos de orden 10 o mayor, rebatiendo la hipótesis del gran Euler. Sólo el de orden 6 es imposible. La noticia fue portada en el New York Times y en Scientific American de noviembre de 1959.
En 1960 Parker diseñó un programa informático que permitía en menos de 45 minutos hacer cuadrados de orden 10 ortogonales a cualquier cuadrado dado.
La llegada de los ordenadores
El trabajo necesario para decidir empíricamente la cuestión aumenta muy rápidamente con el orden del cuadrado y en 1959 rozaba el límite de potencia de los computadores electrónicos.
A partir del 1959, la velocidad de las máquinas computadoras aumenta vertiginosamente, así como el ingenio y la habilidad de los matemáticos encargados de programarlas. Parker diseñó un programa que permitía en 28-45 minutos diseñar cuadrados de orden 10, ortogonales a cualquier cuadrado dado. El factor de optimización del tiempo había sido del orden de 1012 y destinado a crecer.
|
Gráfico sobre la evolución de la velocidad computacional de los ordenadores: Max Roser and Hannah Ritchie, Technological Progress, in ourworldindata.org. Se note que la escala vertical es logarítmica, así que por cada escalón la velocidad es 10 veces la anterior |
Estas investigaciones abrieron nuevas perspectiva en campos como el de los “planos proyectivos finitos” y de los “bloques equilibrados incompletos”
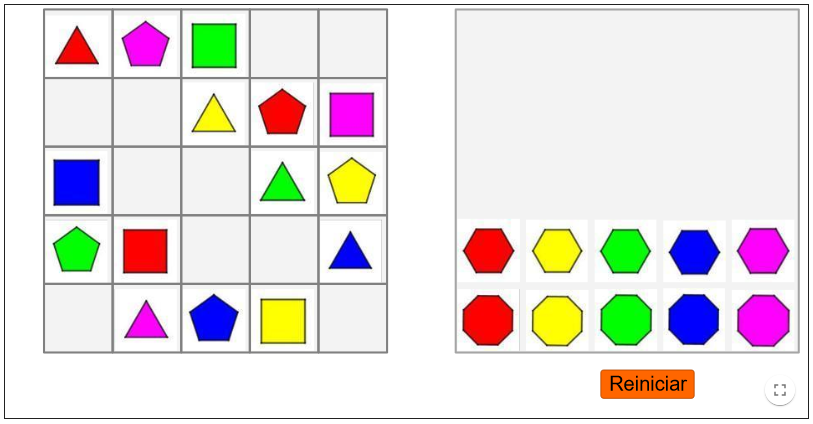
Reto #3: Construir un Cuadrado Grecolatino 5x5
Los cuadrados Grecolatinos en la literatura
Georges Perec (1936-1982) publicó su novela La vida instrucciones de uso en 1978. Una de las fuentes inspiradoras fue el dibujo que Saul Steinberg hizo en 1949 para The Art of Living.

638 páginas, 99 capítulos para componer 6 partes nos conducen, sin pasar dos veces por el mismo sitio, a conocer ambientes, personajes, vidas, pasiones, manías de los inquilinos del edificio situado al nº 11 de la calle Crubellier, simulando un enorme tablero de 10×10 huecos, recorrido con un itinerario marcado por el salto del caballo.
El desarrollo de la novela sigue varios procesos matemáticos formales:
- Recorre el edificio siguiendo los movimientos del caballo de ajedrez adaptados a un tablero de 10×10;
- pseudo-quenina de orden 10
- bicuadrado latino ortogonal de orden 10
- teoría de grafos y recorrido hamiltoniano.
Perec no era el único miembro del OuLiPo Ouvroir de Littérature Potentielle que demostraba un profundo interés hacia las matemáticas. Raymond Queneau (1903-76) era licenciado en matemáticas y fue miembro de la Sociedad Matemática de Francia. Su interés se reveló en especial en dos obras: el Cien mil millones de poemas y los Ejercicios de estilo, que tuvo una primera edición en 1947 y una edición ampliada en 1969. Una potente matemática está presente también en Une histoire modèle.
En las artes plásticas: los cuadrados mágicos
Conocidos ya en la antigüedad, se les atribuyeron propiedades excepcionales y mágicas.
El Cuadrado Mágico de orden 4 que Alberto Durero (1471-1528) pintó en su grabado Melancolía I (1514) tiene como valor constante en cada fila, columna y en las diagonales mayores el número 34.
La constante de un cuadrado mágico es fácil de calcular: basta sumar todos los números y dividir la suma entre el número de filas o de columnas.
1 + 2 + 3 + 4 + … + 16 = 136; 136 : 4 = 34


Pero, en el cuadrado se esconden muchas más maneras de obtener la constante, por ejemplo sumando los 4 números que componen los 4 cuadrados de cada esquina:
16+3+5+10 = 2+13+11+8 = 9+6+4+15 = 7+12+14+1 = ¡34!
¿Hay más? O sí, ¡muchos más: 52 exactamente! Sin contar las que pueden obtener por simetría o permutaciones.
Gaudí puso en la fachada de su Sagrada Familia un cuadrado mágico, obtenido modificando el Cuadrado Mágico de Durero para que la constante fuera 33 –los años de Cristo– y no 34. A su potente valor simbólico no corresponde el mismo interés matemático.

Para citar otro Cuadrado Mágico famoso, existe el Cuadrado Mágico Diabólico, que tiene como constante 666.
Aplicaciones de los CGLs
 Contrariamente a lo que pensaba Euler cuando empezó a estudiar el problema de la distribución de sus 36 soldaditos, los cuadrados grecolatinos han revelado su gran utilidad en distintos campos y por diferentes funciones científicas y tecnológicas.
Contrariamente a lo que pensaba Euler cuando empezó a estudiar el problema de la distribución de sus 36 soldaditos, los cuadrados grecolatinos han revelado su gran utilidad en distintos campos y por diferentes funciones científicas y tecnológicas.
El personaje central de esta nueva etapa es Ronald Aylmer Fisher (1890-1962), biólogo, estadístico, matemático y astrónomo.
Tiene un lugar preminente en la teoría evolucionista, ya que redescubrió las teorías de Mendel para combinarles con la selección natural, creando así una nueva síntesis del Darwinismo.
Trabajando en una estación agrícola experimental, elaboró un análisis de la varianza utilizando la t de Student que permitió el desarrollo de la biometría o estadística médica.
Descubrió la utilidad de los cuadrados grecolatinos para programar experimentos y atenuar los factores de alteración en las investigaciones.
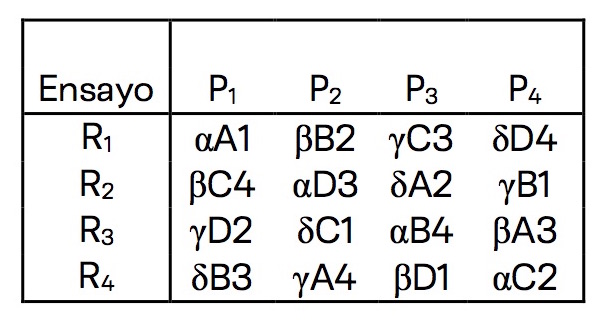
Programación de los ensayos para analizar el desgaste de unos tejidos: A-D: tratamientos; 1-4: tejidos; a-d: agentes desgastantes.
Víctima de sus tiempos, abrazó las teorías maltusianas y estuvo entre los fundadores de la Sociedad de Eugenesia y los promotores de su campaña para la esterilización (voluntaria) sobre la base de criterios eugénicos. Se opuso a la campaña anti racial de la UNESCO, sosteniendo la diversidad de los grupos humanos en su desarrollo intelectual y emocional.
Recientemente, hasta el vitral en el salón comedor de Gonville y Caius College, en Cambridge, Inglaterra, que le conmemoraba, ha sido removido en 2020 por petición popular del movimiento “Black lives matter”.
El diseño experimental factorial
El diseño experimental factorial es una técnica estadística que permite identificar y cuantificar las causas de un efecto dentro de un estudio experimental con unas cuantas variables.
Prescribe una serie de pautas relativas qué variables hay que manipular, de qué manera, cuántas veces hay que repetir el experimento y en qué orden para poder establecer con un grado de confianza predefinido la existencia de una presunta relación de causa-efecto.
El diseño experimental encuentra aplicaciones en la industria, la agricultura, la mercadotecnia, la medicina, la ecología, las ciencias de la conducta, etc. constituyendo una fase esencial en el desarrollo de cualquier estudio experimental. Entre sus aplicaciones:
- Composición para la elaboración de productos químicos, farmacéuticos, alimentares…
- Medida de la variabilidad de instrumentos de control.
- Diseño de electrodos, motores eléctricos, elementos de sujeción.
- Estudios de corrosión, soldadura, mecanización, pintura.
- Optimización de las redes informática, del tiempo de CPU, semiconductores, filtros pasivos.
La aplicación de los cuadrados grecolatinos al diseño de experimentos juega un papel básico en la mitigación de los elementos perturbadores.
Bibliografía
C.I. CÓRTEZ PERÉZ, Propiedades y aplicaciones de los cuadrados mágicos.
GARDNER, Nuevos pasatiempos matemáticos, Alianza Editorial (1972).
IBAÑEZ, Mateadictos: cuadrados mágicos, Blog Ciencia al Pil Pil
MACHO, La vida instrucciones de uso, de Georges Perec, Divulgamat (10/2010).
PIRANI, Quadrati latini e di ordine superiore per la attenuazione dei disturbi nelle attività sperimentali.
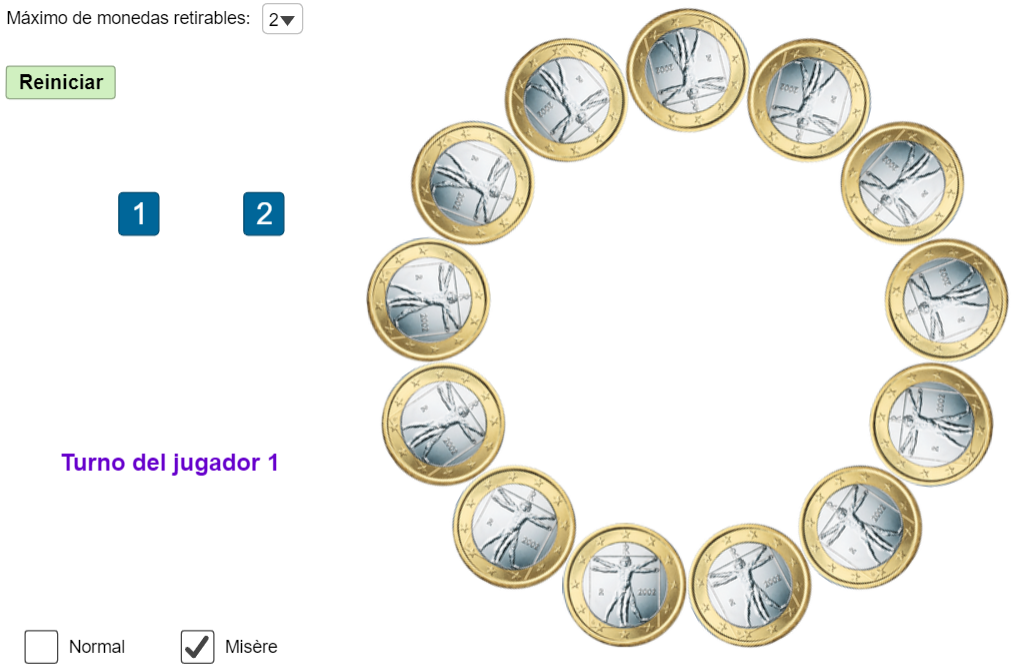
¡A jugar! Juegos relacionados con el cuadrado grecolatino
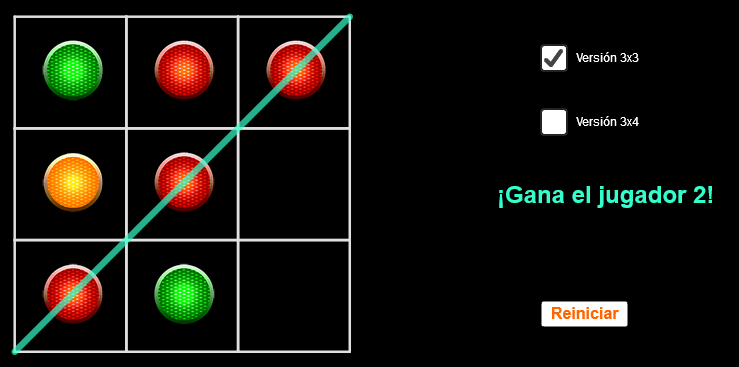
En un panel dedicado a los juegos, no hubiéramos podido dejaros sin jugar, así que usad los enlaces para gozar de estas versiones virtuales de juegos.
Tanto los tableros como las piezas que se mueven son bastante sencillos de dibujar y realizar en vuestras casas o escuelas, si queréis darles un formado físico y manipulable.
Es bastante común encontrar juegos como los que os presentamos en los museos de matemática o en los espacios que los Centros de Ciencia dedican a las matemáticas. Pueden tener formato de módulo, como algunos que exponemos en el Museu de Matemàtiques de Catalunya, o limitar su uso en las “zonas de descanso” (cada vez más comunes, después de su implementación en el Exploratorium de San Francisco) o en las Ferias que se organizan.
Una vez que uno se ha hecho con las reglas y ha jugado unas cuantas partidas, el deseo de encontrar una estrategia ganadora nace espontáneo y nos permite descubrir cuánto se esconde detrás del primero contacto lúdico.
De esta manera, hasta el juego más competitivo adquiere una vocación colaborativa, que sigue siendo el alimento para la mente que nos gusta más, aun sin desdichar el toque de pimienta que aporta la competición.
Maquetas para construir juegos
Para jugar en tu ordenador o tableta
ANEXO
PERMUTACIONES EN CUADRADOS GRECOLATINOS 4 x 4
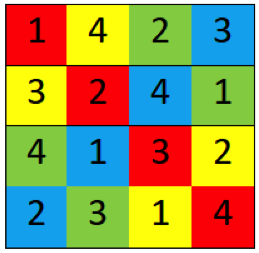 En la investigación de Euler, sus CGL no repetían características en filas y columnas, pero sí en sus diagonales, con unas consecuencias en su resolución que ya hemos comentado.
En la investigación de Euler, sus CGL no repetían características en filas y columnas, pero sí en sus diagonales, con unas consecuencias en su resolución que ya hemos comentado.
Poner la condición de no repetir tampoco en las diagonales representa un reto ulterior en las exposiciones y en las ferias.
Aporta también un estímulo interesante a nivel didáctico, en la busca de estrategias alternativas.
Preparando esta exposición, hemos descubierto una estrategia para pasar del “modelo Euler” al otro, a través de PERMUTACIONES.
Permutaciones de columnas
de ABCD a ACDB.
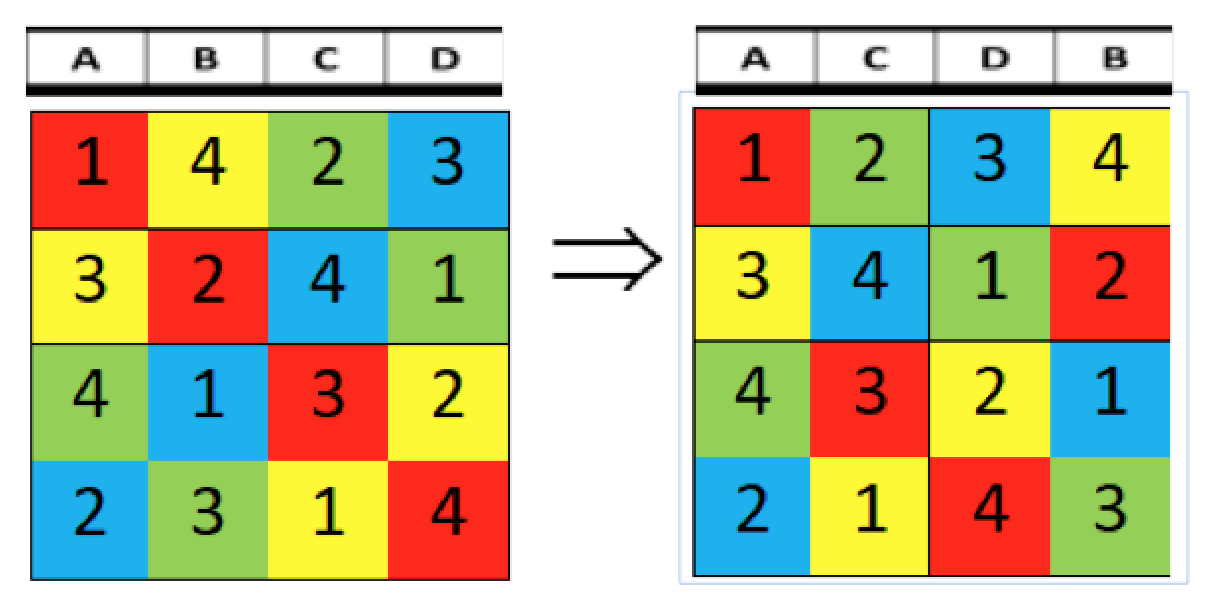
Simplemente desplazando la columna B al final y moviendo las columnas C y D a ocupar el espacio dejado, se resuelve el reto.
Os invitamos a buscar si hay otras permutaciones que resuelven el reto.
Permutaciones de filas
Aplicando el mismo “código” de permutación, de ABCD a ACDB se obtiene un resultado quizás inesperado: en vez de los colores, las diagonales ¡repiten números!
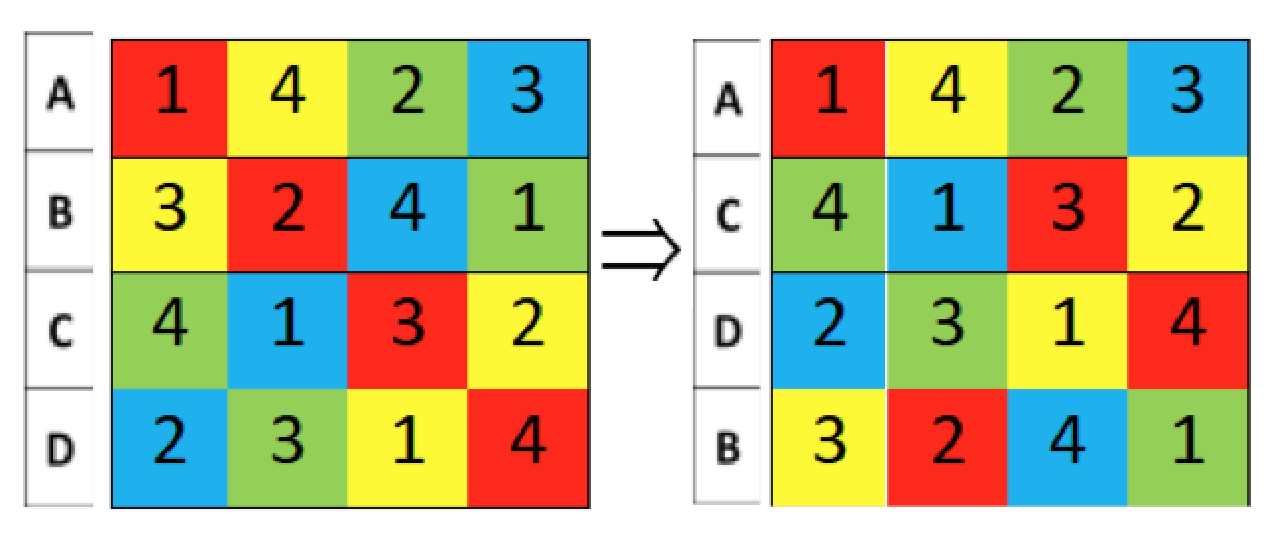
Obviamente, podemos encontrar una permutación distinta que resuelve el reto: de ABCD a BCAD.
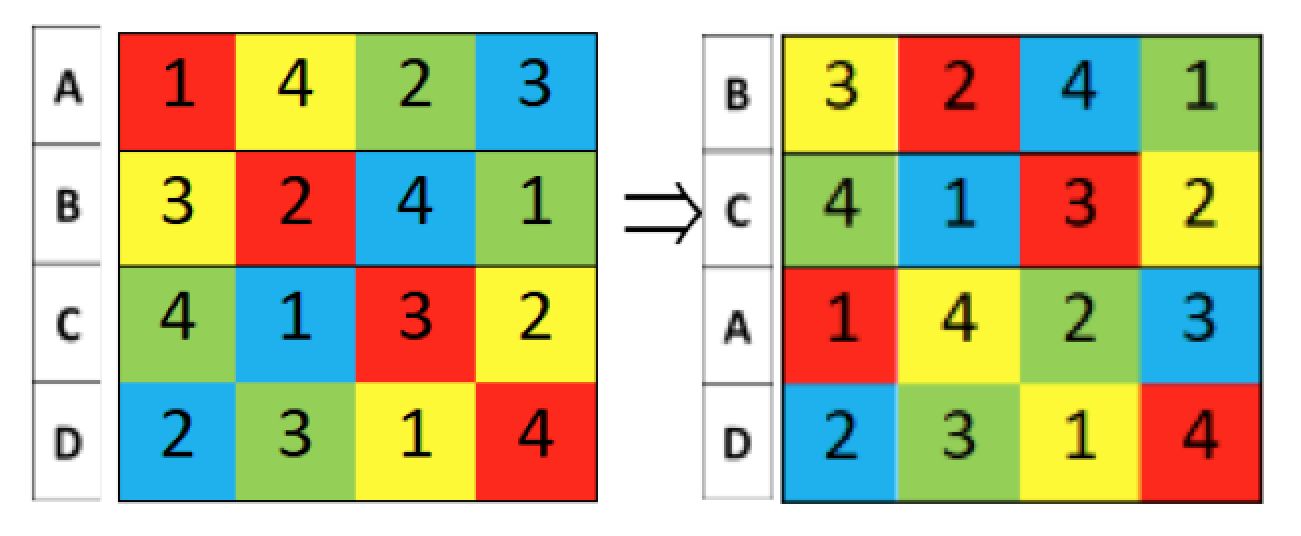
Trabajar con permutaciones es una estrategia muy interesante ya que reduce el número de posibles variaciones. Nuestra investigación puede continuar por las siguientes líneas:
– ¿El sistema funciona con CGL de 5´5 y órdenes superiores?
– ¿Funciona para cuadrados pares y/o impares?
– ¿Tiene relación con las estrategias de resolución de los Sudokus?
– ¿Tiene relación con otros juegos de tablero, como, por ejemplo, el ajedrez?
– ¿Puede ayudar a solucionar otros tipos de retos como el de las 8 reinas?