DESCARGA EL PDF DESCARGA O PDF galego
Autor: José Antonio Mora Sánchez
Aplicaciones interactivas: Bernat Ancochea Millet, José Muñoz Santonja, José Luis Muñoz Casado, José Aurelio Pina Romero y José Antonio Mora Sánchez
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- Presentación
- El arte, el artista y las matemáticas
- La perspectiva. Representar la realidad
- Geometría y armonía en piedra
- Arte islámico. Los geómetras
- Composición y equilibrio
- Y llegó Escher
- Abstracción geométrica
- Escultura
- Arquitectura
- Bibliografía
Presentación
 El arte pretende representar lo que viven las personas, compartirlo con los demás y hacerlo sentir a otros. Unas veces es la realidad lo que intentan reflejar y en otros casos es el producto de su imaginación. Las artes plásticas -pintura, escultura o arquitectura-, han tenido que resolver los problemas derivados de esa representación: el espacio en un plano, conseguir que una composición sea armónica o que un edificio atraiga nuestra mirada a la vez que no se viene abajo… y han recurrido en todas las épocas a las matemáticas para formular esos problemas e intentar darles solución.
El arte pretende representar lo que viven las personas, compartirlo con los demás y hacerlo sentir a otros. Unas veces es la realidad lo que intentan reflejar y en otros casos es el producto de su imaginación. Las artes plásticas -pintura, escultura o arquitectura-, han tenido que resolver los problemas derivados de esa representación: el espacio en un plano, conseguir que una composición sea armónica o que un edificio atraiga nuestra mirada a la vez que no se viene abajo… y han recurrido en todas las épocas a las matemáticas para formular esos problemas e intentar darles solución.
Una pregunta para empezar, ¿qué tiene que ver el cuadro Las Meninas de Velázquez con las matemáticas?
Las aplicaciones del panel virtual Arte y matemáticas se encuentran en un libro de GeoGebra con unos cuarenta applets que intentan poner de manifiesto las conexiones entre las obras de arte y las matemáticas .
El arte, el artista y las matemáticas
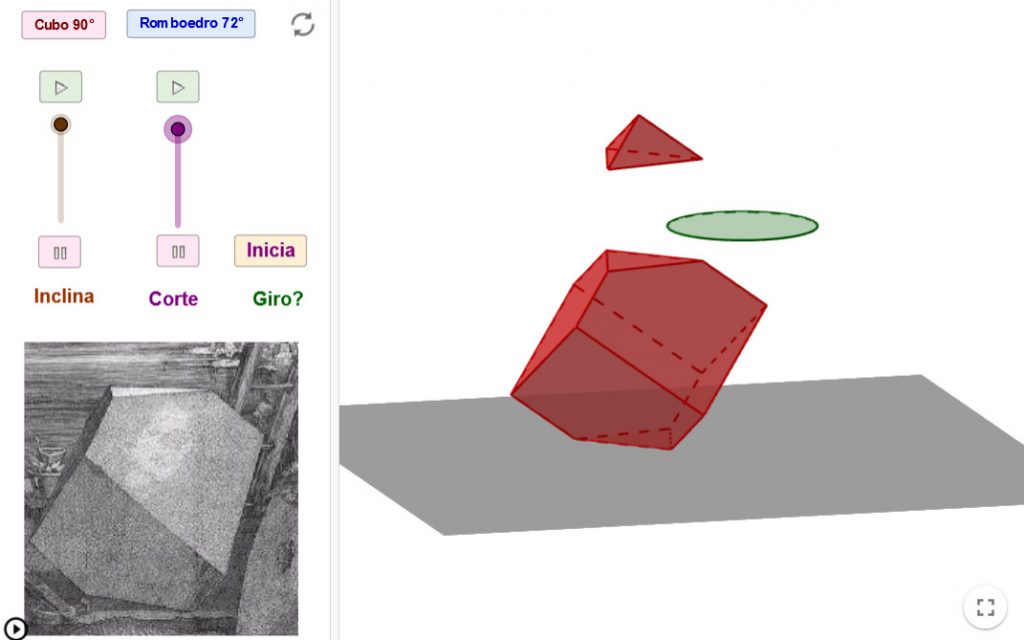
Alberto Durero profundizó en la relación entre arte y matemáticas. En su obra Melancolía I nos muestra una reflexión profunda sobre el arte y el artista. El personaje central tiene en sus manos un compás, representa el carácter pensativo del artista y transmite la insuficiencia del conocimiento humano para conseguir la inspiración y para penetrar en los secretos de la naturaleza. En la pared un cuadrado mágico 4×4 y varios instrumentos de medida y construcción. A la izquierda un poliedro que nos resulta familiar aunque parece tener una parte hundida en el suelo.
¿Qué poliedro representa Durero en el grabado?

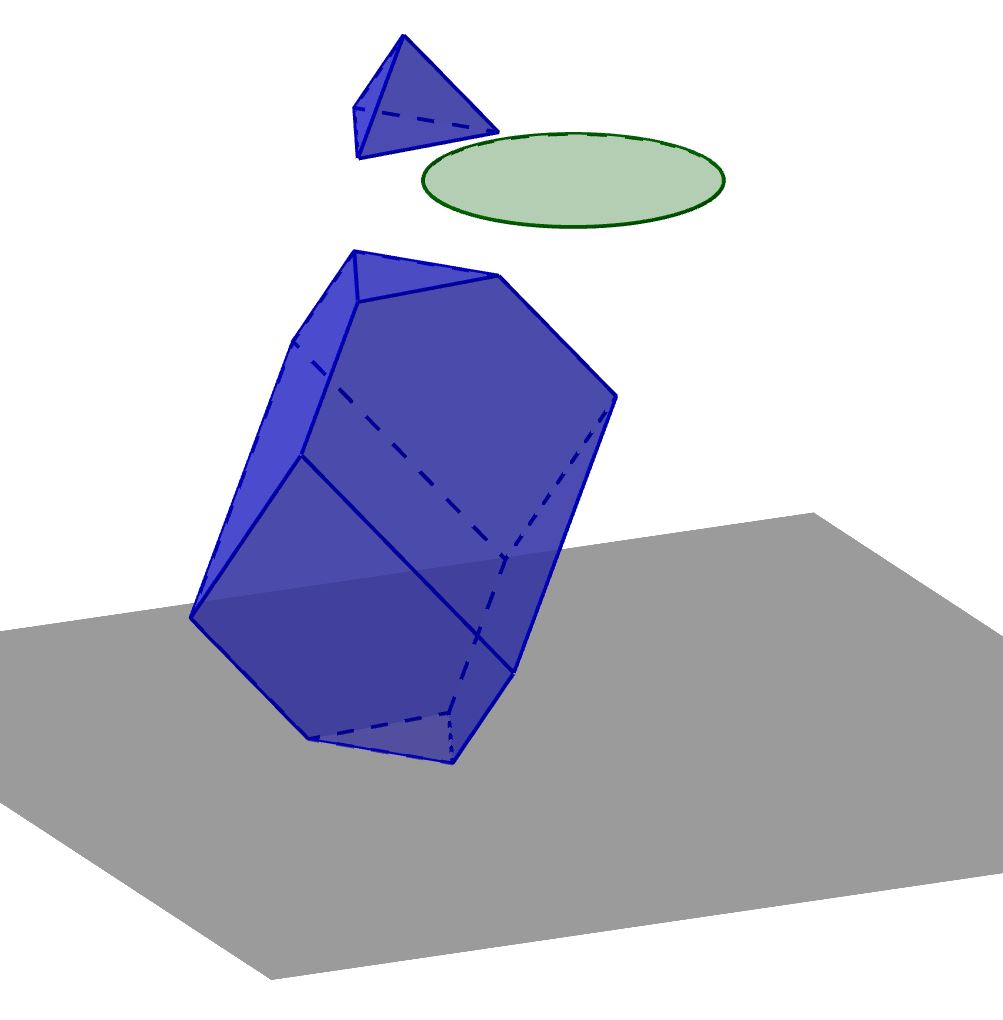
Hacemos que dos poliedros, un cubo y un romboedro, se hundan en la tierra y después realizamos el truncamiento en el vértice superior.
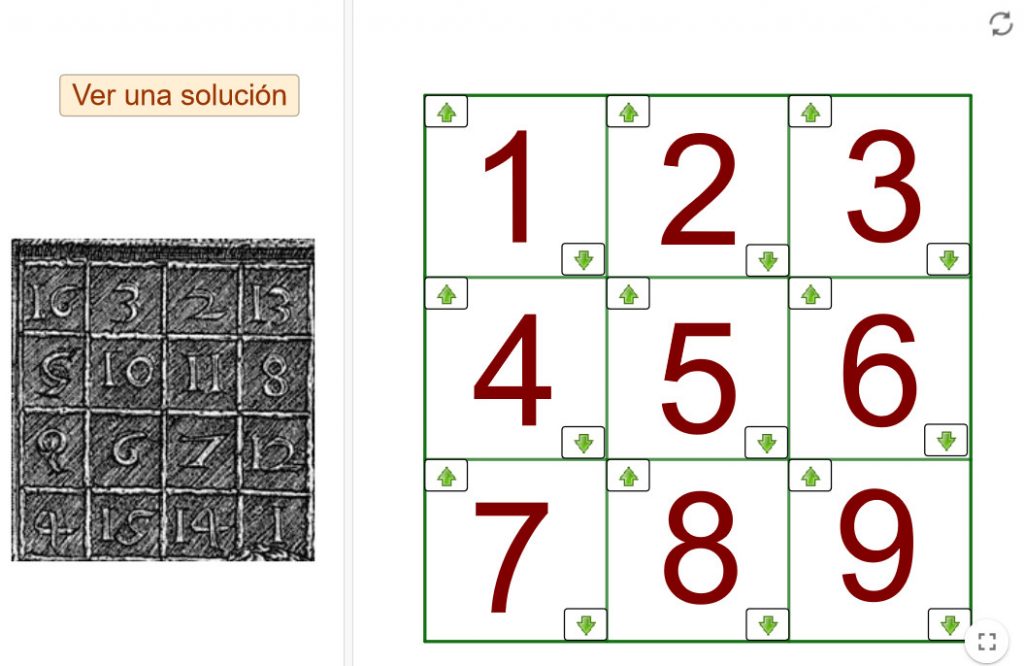
Un applet para que puedas construir tu propio cuadrado mágico 3×3 pincha sobre la imagen. Las flechas arriba y abajo te permiten modificar los números de cada casilla para conseguirlo.
La perspectiva. Representar la realidad
 En el renacimiento las artes plásticas aspiran a representar la realidad. Para que un espacio tridimensional quede reflejado en el plano de un cuadro, el observador debe experimentar la misma sensación que si estuviera viendo la escena real. Los artistas establecen las reglas de la perspectiva volviendo la mirada hacia Euclides. Una de las obras en las que vemos reflejada el estudio de la perspectiva es La última cena de Leonardo Da Vinci. Todos los personajes se encuentran en un mismo plano paralelo al espectador sentados a la mesa. La sensación de profundidad nos la da la construcción de la estancia.
En el renacimiento las artes plásticas aspiran a representar la realidad. Para que un espacio tridimensional quede reflejado en el plano de un cuadro, el observador debe experimentar la misma sensación que si estuviera viendo la escena real. Los artistas establecen las reglas de la perspectiva volviendo la mirada hacia Euclides. Una de las obras en las que vemos reflejada el estudio de la perspectiva es La última cena de Leonardo Da Vinci. Todos los personajes se encuentran en un mismo plano paralelo al espectador sentados a la mesa. La sensación de profundidad nos la da la construcción de la estancia.
Los elementos de la sala representada: el artesonado del techo y las puertas laterales son los que aportan la perspectiva en el cuadro de Leonardo da Vinci.
La perspectiva viene marcada por los edificios del fondo haciendo que cada elemento tenga el tamaño que le corresponde según el lugar que ocupa.
Velázquez complementa la perspectiva geométrica con otras formas de representar la distancia entre los personajes: la perspectiva de color y la de nitidez. Todo parece estar realizado con gran exactitud, pero hay algo que no encaja: los reyes reflejados en el espejo del fondo.
¿Dónde se encuentran los reyes en esa sala para que el pintor los vea ahí reflejados? ¿Los pinta con el tamaño adecuado?
Geometría y armonía en piedra
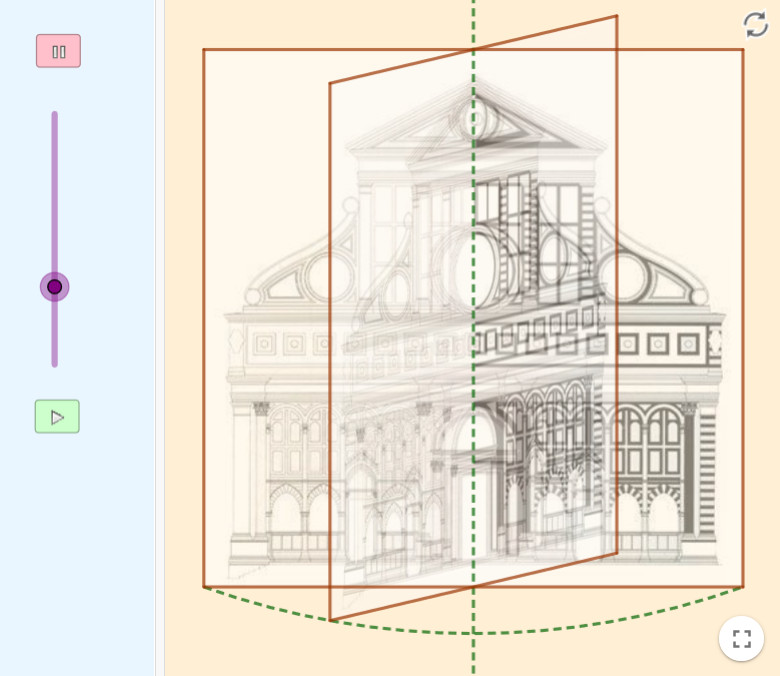
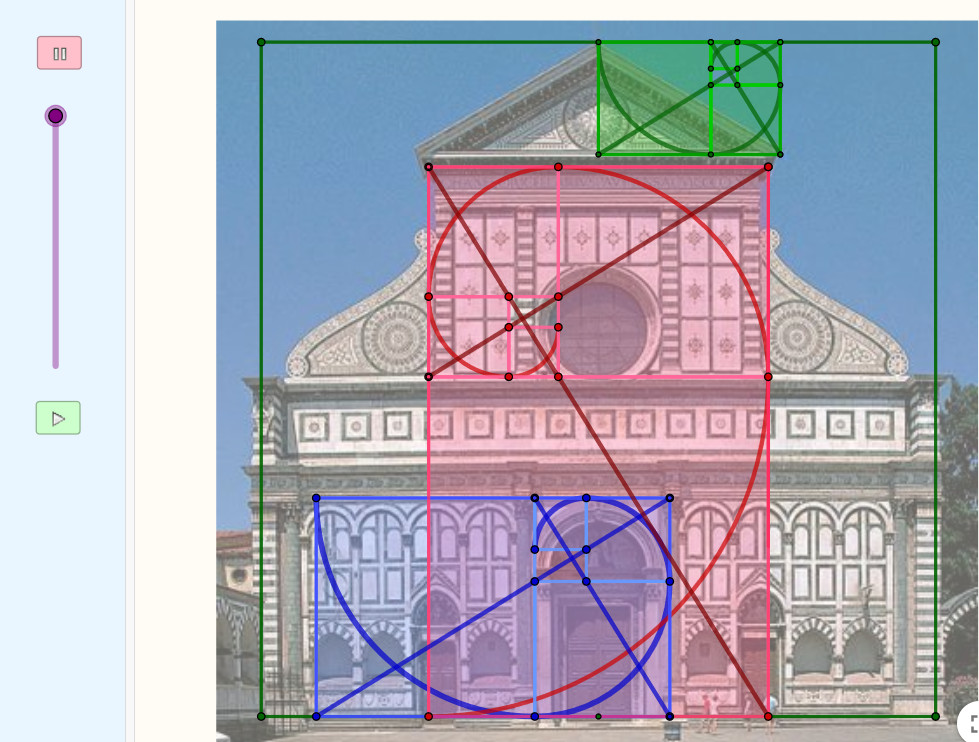
La fachada de Santa María Novella de León B. Alberti reúne la mayoría de los elementos del renacimiento: simetría, estudio de las proporciones y composición geométrica. Se proyecta con las dosis adecuadas de modularidad, proporción, equilibrio, armonía y belleza.
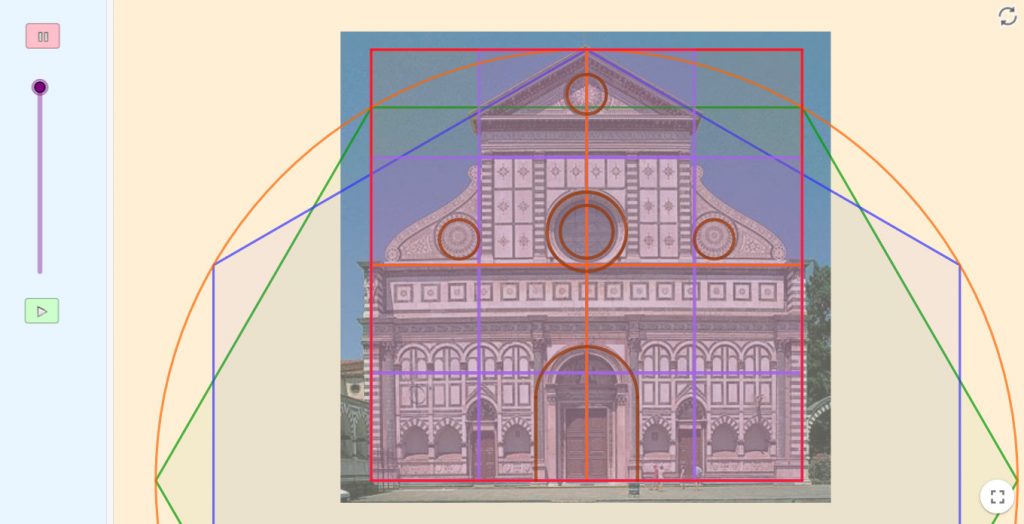
En los applets podemos apreciar la proporción áurea que rige las distintas partes y también las figuras geométricas utilizadas en la composición de sus elementos entre las que destaca el cuadrado como módulo que se repite para formar otros de mayor tamaño 2, 4, 8 y 16 veces más grandes y también podemos reconocer el triángulo, el círculo o el hexágono.
Construimos la mitad de la fachada y “damos la vuelta” a la imagen para componer la fachada completa. El eje de simetría vertical se encarga de hacerlo.
Los elementos geométricos: círculo, cuadrado, y hexágono utilizados para el diseño de la fachada y cómo se relacionan entre ellos para dar lugar a un resultado de gran armonía.
La presencia de la proporción áurea en el diseño de la fachada de Santa María Novella. Para cada secuencia de rectángulos áureos se ha diseñado la espiral correspondiente.
Arte islámico. Los geómetras
En algunas de las regiones en las que se desarrolla el arte islámico no hay ricos materiales como el mármol para construir los grandes edificios institucionales. ¿De qué forma puede un gobernante mostrar su poder ante sus invitados cuando los recibe en un palacio si sus construcciones son de barro cocido?

Encuentran la solución en la cerámica vidriada para decorar completamente las paredes. Los artesanos nazaríes -los geómetras-, utilizaron los movimientos en el plano: traslaciones, giros y simetrías con los que crear diseños complejos resulta una tarea sencilla. Convierten figuras elementales como el cuadrado o el triángulo en bellas composiciones de color.
Los cuatro applets de esta sección toman como base los trabajos de Manuel Martínez Vela reflejados en su libro La Alhambra con Regla y Compás y se han llevado a animaciones de GeoGebra que nos muestran paso a paso la construcción de cada mosaico. La colección de 23 aplicaciones se encuentra en esta dirección.
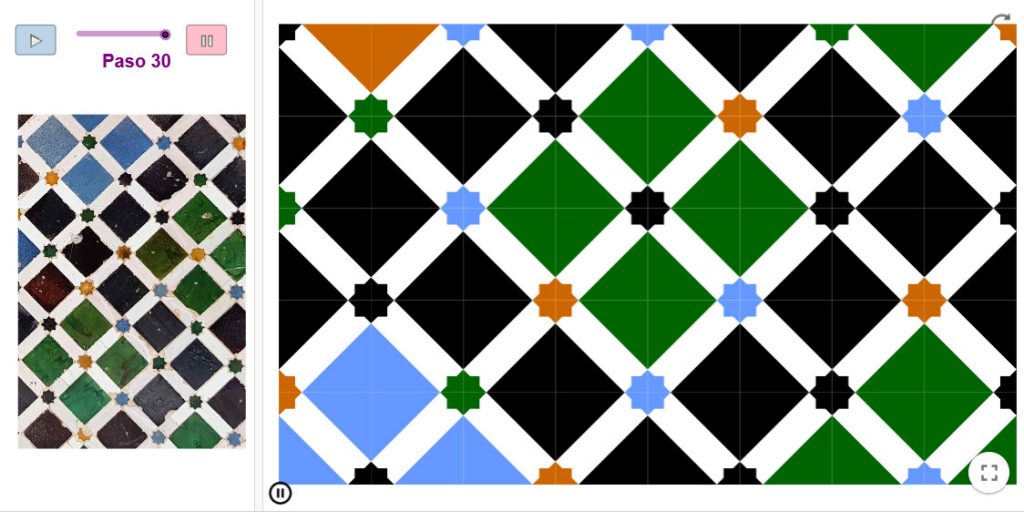
El mosaico de cuadrados del patio de los Arrayanes está formado por cuadrados dentro de cuadrados de colores que a su vez están dentro de cuadrados…
La división de un cuadrado en cuatro partes iguales que se colorean de forma alternativa da lugar a uno de los polígonos más sencillos y elegantes de la Alhambra con forma de hueso.
Un triángulo equilátero con lados curvos se asemeja a una pajarita que cambia de dirección continuamente dando una sensación de movimiento infinito.
El decágono regular y el rombo que se obtiene al prolongar algunos de sus lados. En su interior se esconden varias estrellas de diez y cinco puntas en una bella composición.
Composición y equilibrio
Muchos artistas han utilizado ideas geométricas –a veces puede que de forma inconsciente-, para sus composiciones en la búsqueda del equilibrio entre las distintas partes de la obra, tenemos ejemplos muy claros en El descendimiento de Roger van der Weyden, en Las Meninas de Velázquez, El quitasol de Goya y en muchas obras de Leonardo da Vinci, Rafael, Piero della Francesca, Dalí o Picasso.
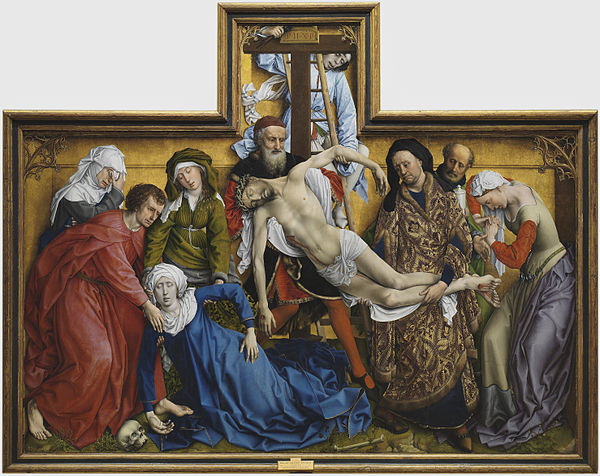
Utilización del cuadrado, el círculo y el pentágono regular en la composición geométrica de la escena del descendimiento.
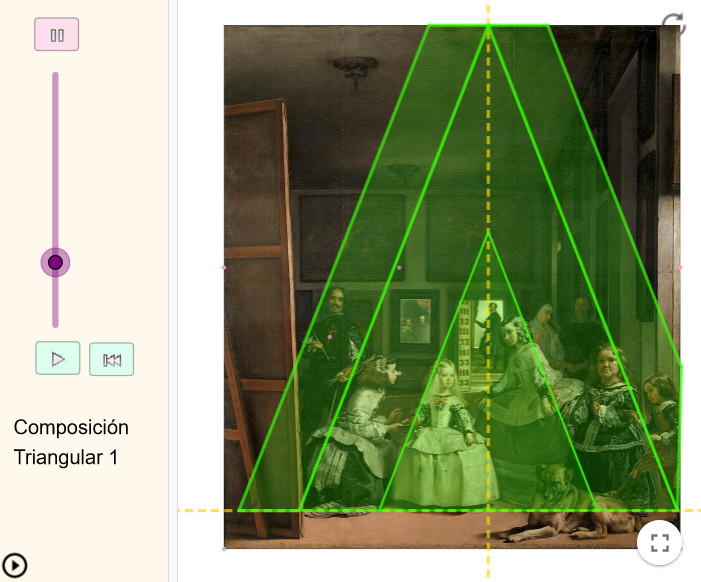
Dos formas de ver la composición triangular en Las meninas de Velázquez siguiendo el rastro de la iluminación de los personajes.
La estructura triangular del cuadro es una de las más claras. Un triángulo isósceles envuelve a los dos personajes y un triángulo semejante al anterior es el que recoge a la mujer sentada.
Y llegó Escher
Las matemáticas ocupan un lugar central en la obra del artista holandés Maurits C.  En sus visitas a la Alhambra estudió los mosaicos nazaríes para crear sus propios mosaicos en los que las figuras se transforman progresivamente, parecen saltar del plano al espacio o se encuentran en el infinito. Llevó al extremo las reglas de la perspectiva para crear mundos que percibimos como reales pero, cuando los analizamos detenidamente, comprobamos que son imposibles.
En sus visitas a la Alhambra estudió los mosaicos nazaríes para crear sus propios mosaicos en los que las figuras se transforman progresivamente, parecen saltar del plano al espacio o se encuentran en el infinito. Llevó al extremo las reglas de la perspectiva para crear mundos que percibimos como reales pero, cuando los analizamos detenidamente, comprobamos que son imposibles.
En las animaciones de esta sección se ha introducido un elemento adicional: generalmente una bola que mantiene las proporciones que dicta la perspectiva propuesta por Escher en su obra y hacemos que recorra los paisajes que representa para hacernos reflexionar sobre los engaños que el autor pone ante nuestros sentidos, en unos casos para desenmascararlos y en otros para añadir más confusión.
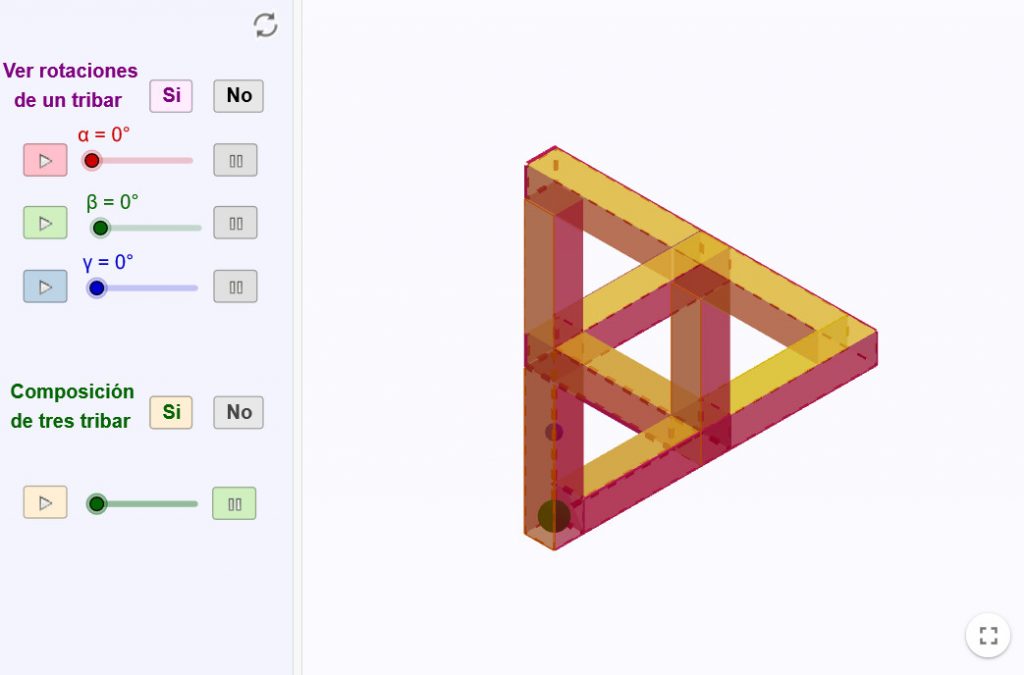
El triángulo imposible de Reutersvärd y Penrose es un objeto compuesto por tres prismas de base cuadrada unidos de tal forma que, visto desde un determinado punto, da la sensación de ser una estructura rígida y conectada. Aquí podemos ver uno solo o varios conectados y conseguimos que una bola circule por su interior haciéndonos creer que se desliza y cae para volver al mismo sitio.
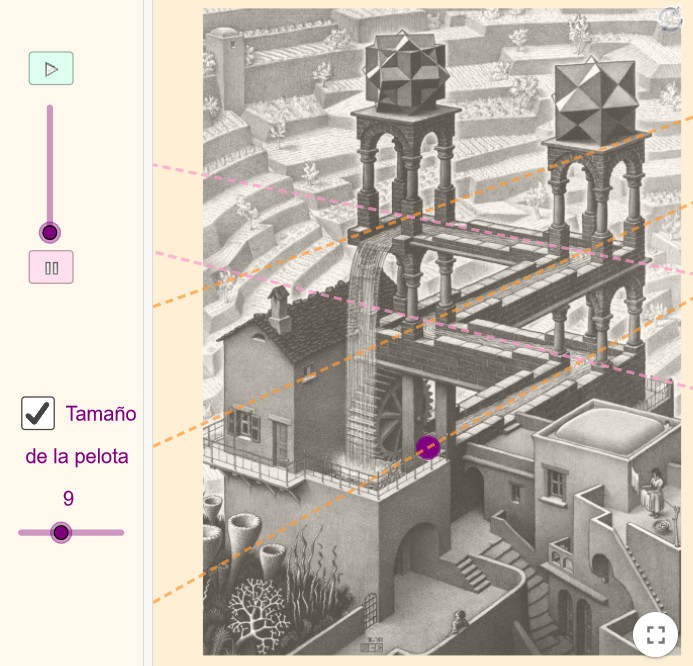
En Cascada utiliza la composición de varios triángulos imposibles de Reutersvärd y Penrose para crear la ilusión de un caudal de agua que fluye descendiendo continuamente hasta dar el salto en la cascada y comprobamos que ha vuelto al inicio, en un ciclo infinito.
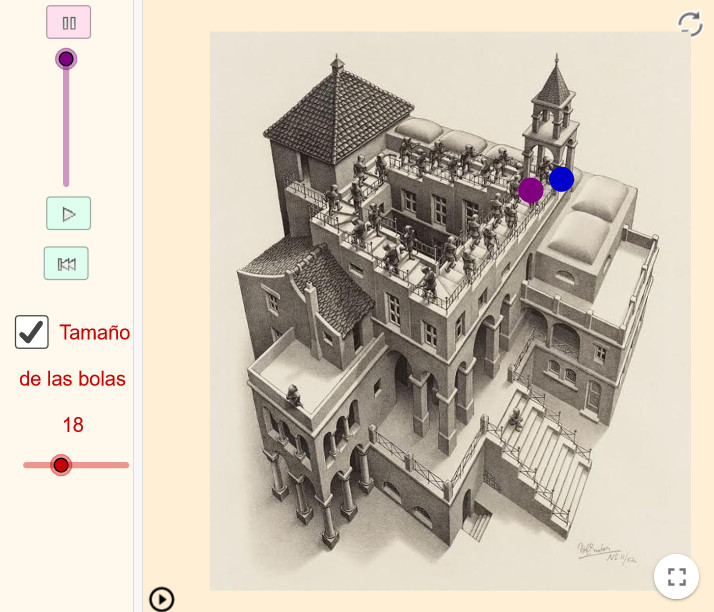
Nos presenta una torre en la que un grupo de monjes o bien no paran de subir (los que van por el exterior) o no paran de bajar (los del interior) en una escalera sin fin. Escher se basa en la escalera imposible de Penrose, la representación en el plano de una escalera que gira cuatro veces 90º y los escalones bajan o suben según se recorra en una dirección u otra.
Escher crea un edificio en el que el suelo, las columnas y el techo nos ponen continuamente en contradicción porque en muchos casos si la base de un pilar parece estar delante, la parte superior está detrás y viceversa. También se presta atención al personaje de la parte inferior izquierda que mantiene un cubo de Necker, una figura indecidible que mantiene en sus manos mientras mira su dibujo en el suelo.
Representa una construcción que parece tener un eje de simetría axial situado en la línea vertical central en el que reina la confusión: paredes que deberían mirar hacia la derecha, lo hacen hacia la izquierda y al revés. Por arte de magia, el suelo se transforma en techo y al contrario.
En Otros Mundos II nos presenta seis ventanas en las que cada suelo puede ser techo de otro mundo. Se ha utilizado la animación de GeoGebra para resaltar esa sensación con una especie de bola (en realidad un círculo, aunque eso es lo menos importante). La bola cae a cámara lenta desde cada techo hasta su suelo y se desplaza en busca de un nuevo techo para volver a caer y seguir buscando otro techo…
En esta obra Escher nos presenta varios mundos que coexisten simultáneamente: terrazas exteriores que dan paso al interior de un edificio nos llevan a situaciones contradictorias. Encontramos en un mismo tramo de escalera a dos personas colocadas en el mismo sentido de la marcha, mientras una sube la otra baja. Es la forma en la que Escher confunde nuestros sentidos y la interpretación nuestro cerebro hace de lo que nos presenta.
Abstracción geométrica
 A principios del siglo XX la utilización de la geometría en la pintura se lleva al extremo de pretender eliminar la representación de cualquier realidad. Evolucionan gradualmente hacia la simplificación de las formas hasta llegar a la abstracción geométrica. Las líneas y las formas conforman una composición abstracta de elementos que invitan a ver en ellos multitud de significados e intenciones de su autor.
A principios del siglo XX la utilización de la geometría en la pintura se lleva al extremo de pretender eliminar la representación de cualquier realidad. Evolucionan gradualmente hacia la simplificación de las formas hasta llegar a la abstracción geométrica. Las líneas y las formas conforman una composición abstracta de elementos que invitan a ver en ellos multitud de significados e intenciones de su autor.
El espectador tiene que aportar las ideas, sentimientos, sensaciones o evocaciones que activa la contemplación de la obra en su mente. En la obra de Piet Mondrian solo importan las formas geométricas elementales, los ángulos rectos y los colores primarios, sus cuadros solo contienen rectángulos de colores básicos separados por líneas negras.
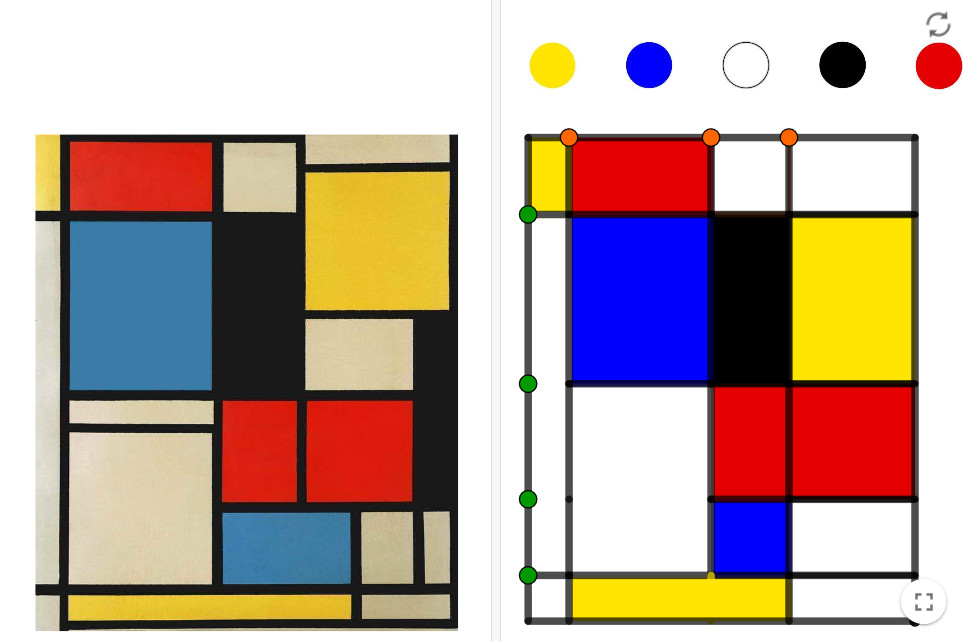
En la obra de Piet Mondrian solo importan las formas geométricas elementales, sus cuadros solo contienen rectángulos de colores básicos separados por líneas negras. En el applet puedes crear tu propio cuadro “a lo Mondrian”, podrás cambiar los colores y las dimensiones de los rectángulos.
¿Cuál debe ser la medida del lado del cuadrado negro y donde debe apoyarse para pasar justo por el centro del cuadrado de color que lo contiene, y a partir de ese cálculo reproducir el cuadro.
En la construcción comprobamos que al girar un conjunto de cubos se pude llegar a construir una figura imposible. Pulsa sobre sobre el botón Play para animar la construcción.
En la construcción comprobamos que al girar un conjunto de cubos se pude llegar a construir una figura imposible.
En el siguiente cuadrado podemos ver como partiendo de un conjunto de cuadrados y rectángulos, con un simple giro, nos da la impresión de pasar a las tres dimensiones.
Obra del pintor Vicente Rodes a partir de un problema de matemáticas propuesto a los alumnos del IES Sant Blai de Alicante. La animación reproduce la trayectoria seguida para dividir el cuadrado en dos mitades y propone otras posibles soluciones.
Escultura
 La abstracción geométrica se lleva también a la escultura del siglo XX con el objetivo de investigar sobre las formas básicas, el rigor, la utilización de las matemáticas, el orden y la modularidad y además se intenta sacar partido de la tercera dimensión. Los escultores intentan aprovechar la posibilidad de movimiento, unas veces haciendo que la obra pueda moverse y en otras consiguen que sea el desplazamiento del propio espectador lo que provoque los cambios en el objeto construido. Los artistas incorporan nuevas tecnologías (en un principio la fotografía, posteriormente los programas de ordenador) y los nuevos materiales (el acero, los plásticos).
La abstracción geométrica se lleva también a la escultura del siglo XX con el objetivo de investigar sobre las formas básicas, el rigor, la utilización de las matemáticas, el orden y la modularidad y además se intenta sacar partido de la tercera dimensión. Los escultores intentan aprovechar la posibilidad de movimiento, unas veces haciendo que la obra pueda moverse y en otras consiguen que sea el desplazamiento del propio espectador lo que provoque los cambios en el objeto construido. Los artistas incorporan nuevas tecnologías (en un principio la fotografía, posteriormente los programas de ordenador) y los nuevos materiales (el acero, los plásticos).
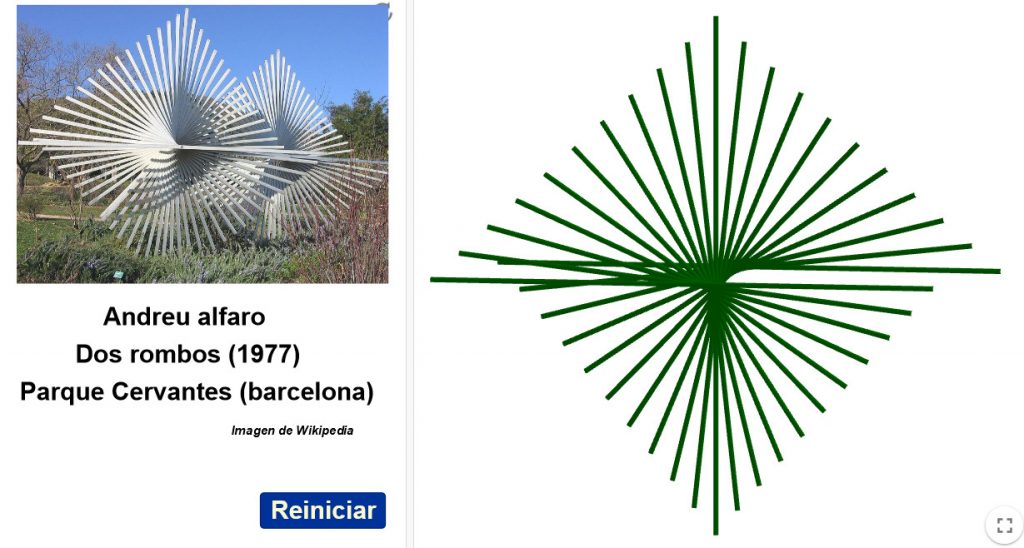
Composición que parte de un dodecaedro central de acero inoxidable que gira alrededor de uno de sus ejes de rotación. De cada una de las doce caras salen perpendicularmente 51 barras de acero.
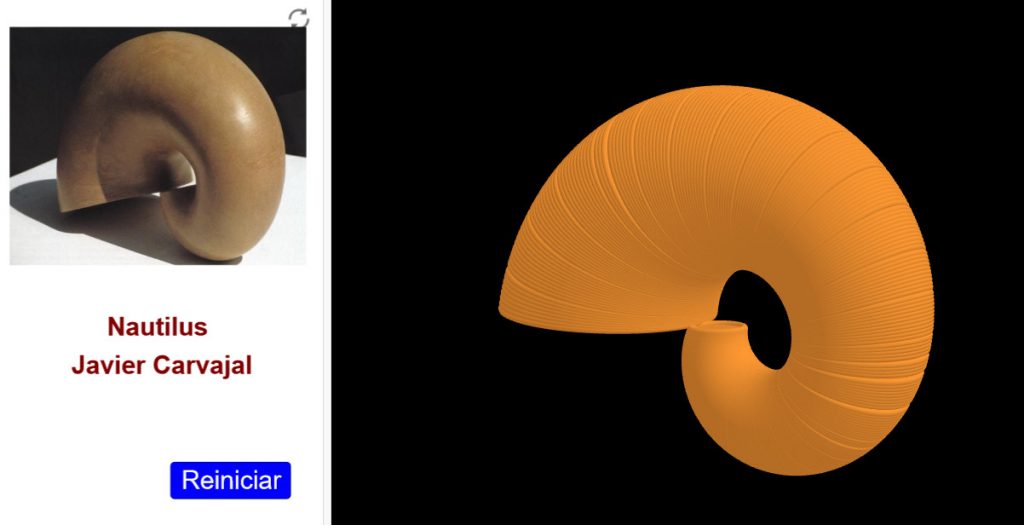
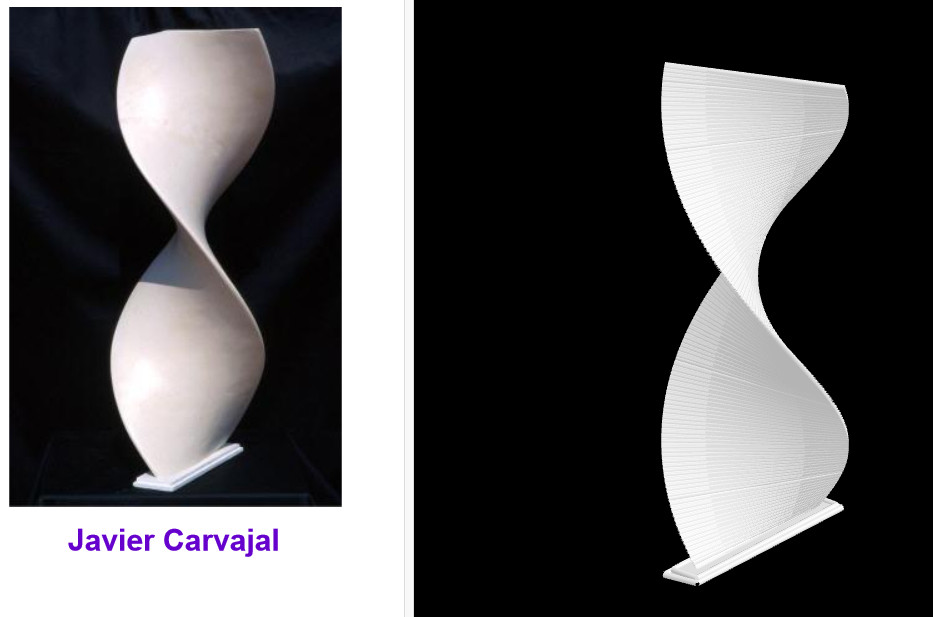
Un segmento gira a la vez que se traslada en el espacio en una dirección perpendicular y modifica su longitud para conseguir eun determinado efecto visual.
Un círculo se mueve en el espacio. Su centro se desplaza por una curva en forma de espiral a la vez que su radio crece. Cuando el círculo se vuelve a encontrar en el mismo plano que el inicial, las dos circunferencias son tangentes.
Arquitectura
La arquitectura clásica ha tenido que resolver los problemas propuestos por las grandes  construcciones con unos medios limitados por la tecnología de la época. Los anudadores egipcios utilizaban cuerdas con nudos para trazar perpendiculares mediante triángulos rectángulos (lados 3, 4 y 5) en una clara referencia al teorema de Pitágoras. En la edad media resuelven los problemas derivados de la construcción de grandes catedrales con arcos, columnas y cúpulas consiguiendo que los pesos se desplacen de forma equilibrada de unos sitios a otros para que aún hoy sigan en pie. Por otra parte en todas las épocas ha habido la búsqueda de un canon de belleza ideal basado en las proporciones entre las partes y el conjunto del edificio en la que la proporción áurea ha tenido un importante papel.
construcciones con unos medios limitados por la tecnología de la época. Los anudadores egipcios utilizaban cuerdas con nudos para trazar perpendiculares mediante triángulos rectángulos (lados 3, 4 y 5) en una clara referencia al teorema de Pitágoras. En la edad media resuelven los problemas derivados de la construcción de grandes catedrales con arcos, columnas y cúpulas consiguiendo que los pesos se desplacen de forma equilibrada de unos sitios a otros para que aún hoy sigan en pie. Por otra parte en todas las épocas ha habido la búsqueda de un canon de belleza ideal basado en las proporciones entre las partes y el conjunto del edificio en la que la proporción áurea ha tenido un importante papel.
La fachada principal del Partenón se puede enmarcar en un rectángulo áureo. La construcción de la espiral áurea eliminando cuadrados para encontrar nuevos rectángulos áureos y diseñar la espiral áurea hace que nos vayamos encontrando distintos elementos arquitectónicos a cada paso.
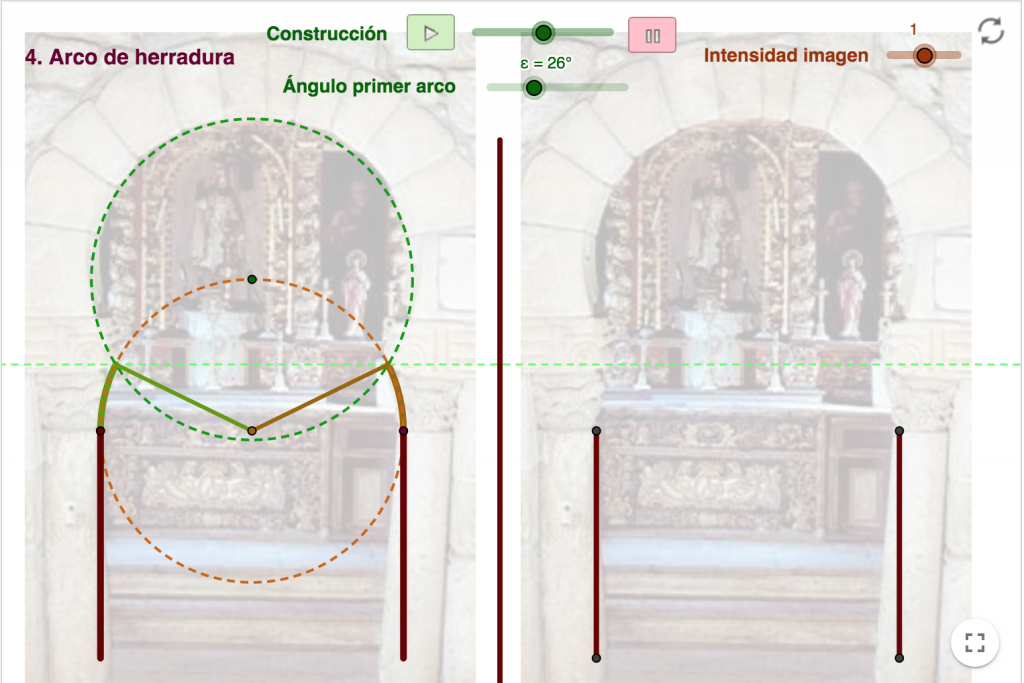
Arco de herradura en la iglesia de San Pedro Balsemao en Lamelgo, Portugal.
Los arcos se utilizan para abrir huecos en un edificio con el fin de abrir una puerta o una ventana mientras se descarga el peso de la construcción para dirigirlo hacia los laterales. El arco de herradura se construye a partir de dos circunferencias.
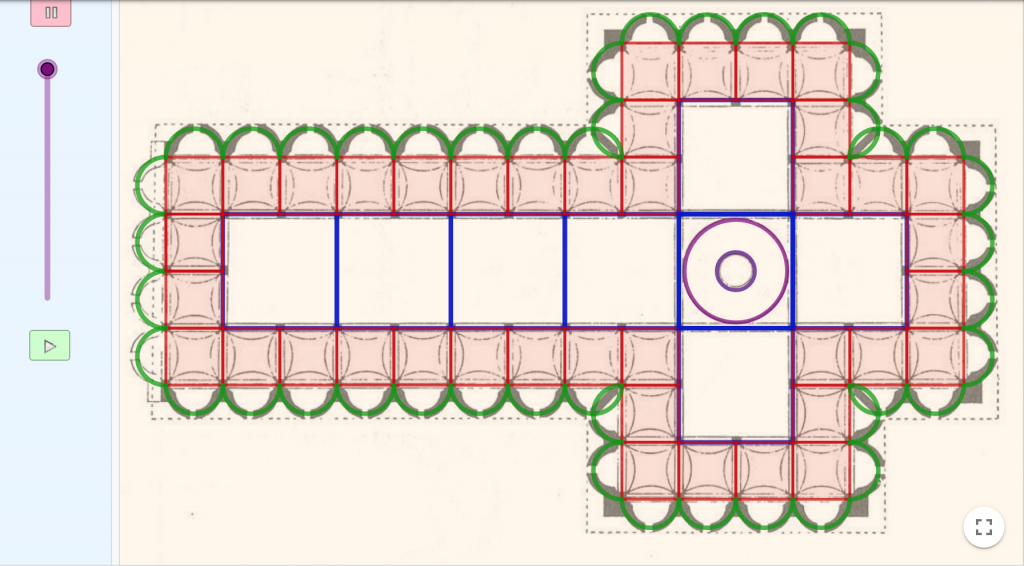
La basílica del Santo Spirito de Florencia utiliza el cuadrado como unidad de medida para la planta. Ocho cuadrados componen la cruz. La altura de la nave es el doble del lado de ese cuadrado mientras las naves laterales se construyen con cuadrados de lado la mitad
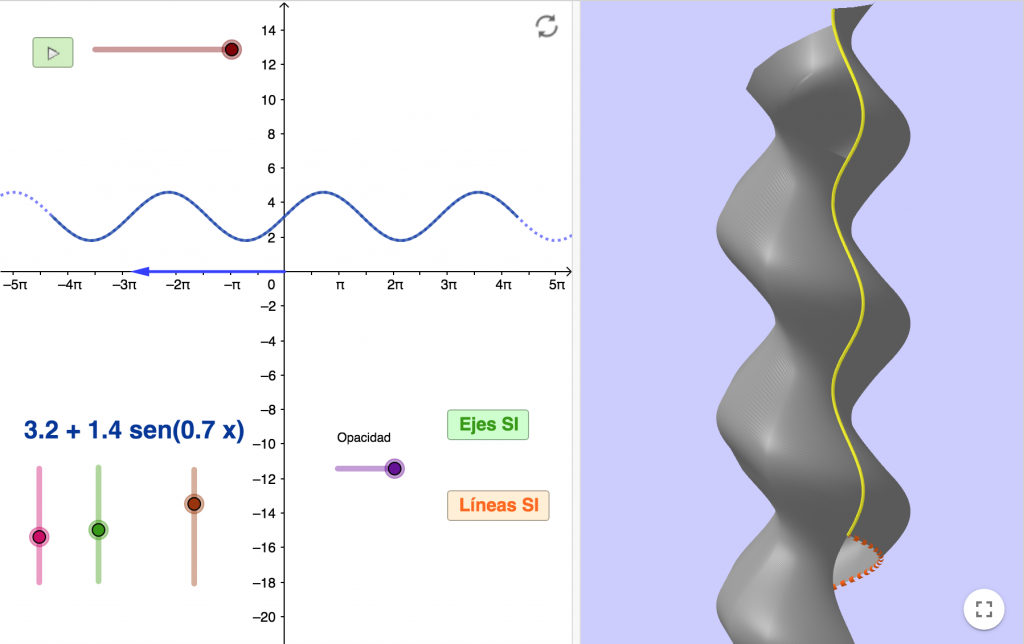
Columna salomónica de la portada del ayuntamiento de Alicante. Sobre el plano XY (z=0) se construye una función trigonométrica que se hace girar en la tercera dimensión alrededor del eje X (colocado verticalmente) a la vez que se traslada con un vector paralelo a ese mismo eje.
Para el Baptisterio de Florencia se ha realizado un applet que permite realizar algunos cambios para modificar la cúpula del edificio.
Columna salomónica de la portada del ayuntamiento de Alicante. Sobre el plano XY (z=0) se construye una función trigonométrica que se hace girar en la tercera dimensión alrededor del eje X (colocado verticalmente) a la vez que se traslada con un vector paralelo a ese mismo eje.
Bibliografía
Bouleau, Charles (1996). Tramas. La geometría secreta de los pintores. Ed. Akal. MadridCapdevila Ed. (1992). Las claves de la pintura. Ed. Planeta. Barcelona.
Ernst, B. (1989). El espejo mágico de M.C. Escher, Taco, Berlín.
Livio, M. (2006)La proporción áurea. La historia de phi, el número más sorprendente del mundo, Ariel, Barcelona.
Martín Casalderrey, F. (2010). El arte visto con ojos matemáticos. Ed. RBA.
Martínez Vela, M. (2017). La Alhambra con Regla y Compás. Ed. Almizate. Alcalá la Real, Jaén.
Meavilla, V. (2007). Las matemáticas del arte. Ed. Almuzara.
Meisner, G.B. (2019). La proporción áurea. Ed. Librero.
Mora, J.A. (2007).Geometría dinámica para el análisis de obras de arte. Revista UNIÓN núm 9.
Mora, J.A. (2017). Azulejos con GeoGebra en el museo de Onda. Revista UNO núm 44, pp 24-33.
Perelló, A.M. (1987). Las claves de la arquitectura. Ed. Ariel. Barcelona.