DESCARGA EL PDF castellano DESCARREGA EL PDF català DESCARGA O PDF galego
Autor: Antonio Pérez Sanz
Aplicaciones interactivas: Manuel Sada Allo y Rafael Losada Liste
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- La geometría de la Naturaleza
- Autosimilitud
- Objetos fractales
- Dimensión fractal
- Copo de nieve de Koch
- Longitud fractal
- La superficie de Marte es un objeto fractal
- Conjuntos de Julia
- Conjunto de Mandelbrot
- Determinismo o azar
- Teoría del Caos
- La extraña bifurcación de la función logística
- La Mariposa de Lorenz
- Fractales y caos
- Actividades
- Bibliografía
“La práctica totalidad de los patrones comunes en la Naturaleza son irregulares. Su aspecto es exquisitamente desigual y fragmentario…”
Benoît Mandelbrot
La geometría de la Naturaleza
Imagínate que estás en plena naturaleza, ante tus ojos un fabuloso paisaje de montaña. Un frondoso bosque refresca el ambiente; al fondo una cadena de montañas en forma de sierra rasga el horizonte y sobre ellas unas nubes blancas adornan el cielo.
 Difícilmente podemos representar este paisaje utilizando la geometría clásica de rectas, planos y curvas elementales, la geometría de Euclides (325-265 a. de C.).
Difícilmente podemos representar este paisaje utilizando la geometría clásica de rectas, planos y curvas elementales, la geometría de Euclides (325-265 a. de C.).
Esta geometría, la euclídea, creada hace más de dos milenios, nos sirve muy bien para describir el mundo artificial creado por el hombre compuesto de edificios y estructuras basadas en líneas rectas, en planos perpendiculares o paralelos, en círculos y en esferas. Nuestras construcciones, nuestros muebles, nuestros instrumentos y diseños son, en su inmensa mayoría objetos de diseño euclídeo.
El matemático Benoît Mandelbrot (Varsovia 1924 – Massachusetts 14 de octubre de 2010), uno de los creadores de la geometría fractal, y el principal protagonista del auge y expansión de esta geometría y de su popularización, nos dice en su libro Introducción a la geometría fractal de la Naturaleza:
 Las nubes no son esferas, las montañas no son conos, las costas no son círculos, las cortezas de los árboles no son lisas y los relámpagos no se desplazan en línea recta…
Las nubes no son esferas, las montañas no son conos, las costas no son círculos, las cortezas de los árboles no son lisas y los relámpagos no se desplazan en línea recta…
Estos objetos y casi todos los que encontramos en plena naturaleza son profundamente irregulares, muy alejados de la extrema regularidad de los objetos de la geometría clásica. Sin embargo, todos estos objetos, las nubes, los relámpagos, los árboles, las costas…, tienen dentro de su irregularidad un orden asombroso. Todos tienen una propiedad fascinante: sus formas se repiten a distintas escalas dentro del mismo objeto.
Autosimilitud

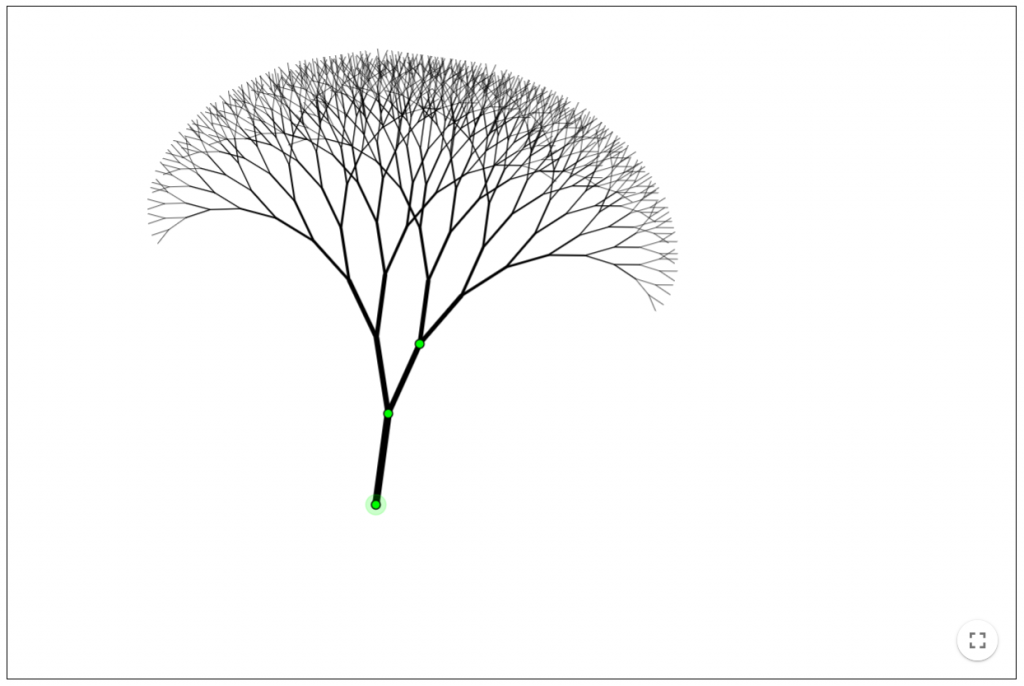
La nube conserva la misma apariencia si la contemplamos entera o si observamos una pequeña parte de la misma. 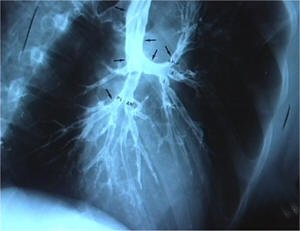 Las ramas de un árbol o las hojas de un helecho reproducen a menor escala la estructura de la planta entera. Algo similar ocurre con las ramificaciones de nuestras venas y arterias y de los bronquios de nuestros pulmones.
Las ramas de un árbol o las hojas de un helecho reproducen a menor escala la estructura de la planta entera. Algo similar ocurre con las ramificaciones de nuestras venas y arterias y de los bronquios de nuestros pulmones.
En todos estos casos, al aumentar la escala con la que vemos el objeto, las irregularidades, en lugar de suavizarse, parece que se mantienen al mismo nivel, semejante al modelo entero.
Esta propiedad, tan difundida en la naturaleza fue bautizada por Mandelbrot como autosimilitud o autosemejanza.
Y también acuñó la palabra fractal para designar a estas configuraciones irregulares y autosemejantes.
Objetos fractales
En la geometría clásica los objetos tienen dimensiones enteras: una línea es de dimensión uno; un triángulo o un círculo y todas las formas planas tienen dimensión dos; una esfera, un cilindro o un poliedro son tridimensionales.
En cambio, las curvas fractales pueden serpentear tanto dentro de un plano que casi llegan a rellenar las dos dimensiones del plano. Es una línea, por tanto, según la geometría euclídea su dimensión debe ser uno. Pero casi rellena el plano, es decir su dimensión también debería ser dos.
Veamos cómo se construye una curva fractal: la curva de Hilbert (1862-1943). Utilizamos un método denominado iteración que consiste en repetir un mismo proceso de forma sucesiva.
Partimos de un cuadrado unidad, lo dividimos en cuatro cuadrados y unimos sus centros (orden 1). Volvemos a dividir cada cuadrado anterior en otros cuatro y unimos los centros mediante una línea poligonal (orden 2). Repetimos el proceso mediante la siguiente iteración (orden 3).
Si repetimos el proceso indefinidamente, en el límite obtendríamos una curva continua que pasaría por todos los puntos del cuadrado unidad.
La curva final es una línea, por tanto, según la geometría euclídea su dimensión debe ser uno. Pero, a su vez, rellena el plano, es decir su dimensión debería ser dos. Estamos ante un objeto que es algo más complejo que una simple línea, al menos como las concebimos ordinariamente.
Por esta propiedad se asigna a estas curvas dimensiones fraccionarias, números comprendidos entre uno y dos. Cuanto más serpentee más próxima estará su dimensión a dos. La curva de Hilbert llega a llenar todo el plano, su dimensión es 2. Si por el contrario zigzaguea poco se parecerá una línea simple y su dimensión estará próxima a uno.
Dimensión fractal
La dimensión fractal se basa en la dimensión Hausdorff H(X) de un objeto fractal X y mide el número N de conjuntos de longitud L que hacen falta para cubrir X utilizando objetos de esa longitud L.
Si comenzamos con un segmento de longitud 1, y lo dividimos en segmentos de longitud L obtendremos N(L) partes, de manera que
![]()
cualquiera que sea L:
![]()
Esta relación está clara en el caso de un segmento rectilíneo. El exponente al que va elevado L nos da la dimensión, en este caso d = 1.
Si el objeto inicial es un cuadrado de superficie 1, y lo comparamos con unidades cuadradas, cuyo lado tenga de longitud L, el número de unidades que es necesario para recubrirlo N(L), cumple
![]()
cualquiera que sea L. En este caso d = 2

En general,

Veamos la dimensión del triángulo de Sierpinski.






Observa la segunda figura: el lado de cada triángulo es L = 1/ 2; para cubrir la figura necesitamos 3 triángulos, es decir N(L) =3
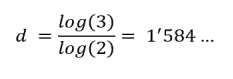
Copo de nieve de Koch
La curva conocida como copo de nieve de Koch en homenaje a su creador, el matemático noruego Niels von Koch (1870 – 1924) que la presentó en sociedad en 1904, se obtiene partiendo de un triángulo equilátero en el que dividimos cada lado en tres partes, quitamos el segmento central y sobre el hueco levantamos otro triángulo equilátero.
Iteramos el proceso y obtenemos el famoso copo de nieve.



Su contorno es verdaderamente intrincado. Entre dos puntos por muy próximos que estén hay infinitos zigzags, es decir, la longitud entre dos puntos es infinita y sin embargo la curva encierra un área limitada. 1,6 veces la del triángulo original. El contorno es verdaderamente intrincado. Entre dos puntos por muy próximos que estén hay infinitos zigzags, es decir, la longitud entre dos puntos es infinita y sin embargo la curva encierra un área limitada. 1,6 veces la del triángulo original.
Veamos la dimensión de la curva de Koch
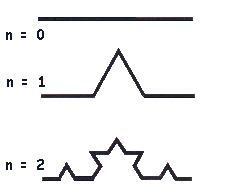
Observemos el caso n=1. La unidad de longitud, es decir, la longitud de cada uno de los segmentos es L = 1/3. El número de segmentos para cubrir la curva es 4. Así la dimensión de la de la curva de Koch es:
d = log(4)/log(3) = 1’2618…
No es de extrañar que los matemáticos del principio de siglo llamasen a esta y otras curvas similares «monstruos matemáticos«.
Longitud fractal
En 1967 Mandelbrot publicó en la revista Science su artículo How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension (¿Cuánto mide la costa de Gran Bretaña? Autosimilitud estadística y dimensión fractal) provocando la sorpresa de todos los lectores.
 Porque esta es una pregunta sin respuesta.
Porque esta es una pregunta sin respuesta.
Dependerá del segmento que tomemos como unidad, de la escala del zoom que utilicemos. La longitud no es la misma si la medimos con segmentos de 1 km o con segmentos de 10 cm. La única respuesta posible sería infinito, pero sólo en el caso de que pudiésemos utilizar un segmento unidad infinitamente pequeño.
La longitud no es la misma medida a escala de un metro, el paso de un hombre, que a escala de un milímetro, el paso de una hormiga.
La longitud no es algo absoluto. Es algo relativo a la escala con la que se mide el objeto.
La costa de Inglaterra es un objeto fractal. De hecho, la similitud de un litoral con la curva de Koch u otras curvas fractales de distinta dimensión ha permitido «medir» lo accidentado de una costa mediante la dimensión fractal de la curva que más se le asemeje. Por cierto, la dimensión fractal del litoral británico es de 1,25.
La superficie de Marte es un objeto fractal
 Por procedimientos análogos utilizando superficies fractales se puede determinar el nivel de rugosidad de la superficie de los planetas. La superficie terrestre tiene una dimensión fractal 2,1 en cambio la dimensión fractal de Marte es de 2,4.
Por procedimientos análogos utilizando superficies fractales se puede determinar el nivel de rugosidad de la superficie de los planetas. La superficie terrestre tiene una dimensión fractal 2,1 en cambio la dimensión fractal de Marte es de 2,4.
Marte es bastante más accidentado que nuestro planeta. La ausencia de océanos líquidos contribuye a ello de forma determinante.
Conjuntos de Julia
El proceso de iteración se puede hacer sobre objetos geométricos o sobre números mediante funciones sencillas. En el fondo se trata exclusivamente de hacer miles o millones de veces las mismas operaciones, en las que el dato de partida de cada paso es el resultado obtenido en el paso anterior. Y esto es lo que realizan a la perfección los ordenadores.
El matemático francés Gaston Julia (1893-1978) está considerado como el precursor de los fractales. Julia estudió las iteraciones de funciones sencillas como ésta:
z -> z2 + c,
donde c es constante. z y c son números complejos, es decir, puntos del plano.
Pintó de blanco los puntos del plano correspondientes a valores de z que en la iteración se alejaban cada vez más del origen, se iban a infinito. Y pintó de negro los que se mantenían en una región acotada del plano complejo.

Si cambiaba la fórmula de partida obtenía otros objetos igualmente extraños. La geometría euclídea no servía para describirlos.Gaston Julia pensaba que la frontera debía ser una línea simple. Sin embargo, cuál no sería su sorpresa cuando sobre su papel -esto ocurría durante la primera guerra mundial y, por supuesto, aún no había ordenadores- fueron apareciendo figuras extrañas de una complicada belleza.
Conjunto de Mandelbrot
Benoît Mandelbrot (1924-2010) modificó la iteración de Julia, f(z) = z2 +c fijando el punto inicial z0 = (0,0) y variando el punto c.
Asignando el color negro a los valores de c que mantienen la sucesión acotada y asignando colores según la velocidad con que la sucesión tiende a infinito en los otros puntos se obtiene el objeto más bello e intrigante del universo matemático.


Si el punto se dispara a infinito no pertenece al conjunto de Mandelbrot, en caso contrario sí. Y la frontera entre los puntos que pertenecen al conjunto y los que están fuera, lejos de ser una línea simple, adquiere unos niveles de complejidad increíbles.
Un zoom por distintas regiones del conjunto de Mandelbrot y una apropiada selección de los colores nos llevará a imágenes de ensueño, sorprendentes por su complejidad y belleza. Y sorpresa, en los sitios más insospechados vuelve a resurgir la silueta familiar del conjunto entero.

La rugosidad de dicha frontera, lejos de suavizarse al hacer sucesivas ampliaciones, nos muestra formas cada vez más complicadas y atrayentes que de vez en cuando nos reproducen el original. La exploración de todos los detalles de este magnífico objeto fractal nos podría llevar toda una vida.


El matemático inglés Michael Barnsley consiguió mediante un sencillo programa una réplica casi exacta de una hoja de helecho.
Hoy, con un simple ordenador personal podemos jugar a ingenieros genéticos generando simulaciones de las ramificaciones de nuestras propias plantas o creando nuestros propios paisajes fractales.
En las últimas décadas miles de matemáticos y de informáticos se han dedicado a iterar otras funciones obteniendo un espectacular muestrario de figuras fractales, muchas de las cuales nos recuerdan de una forma increíble a objetos de la naturaleza.
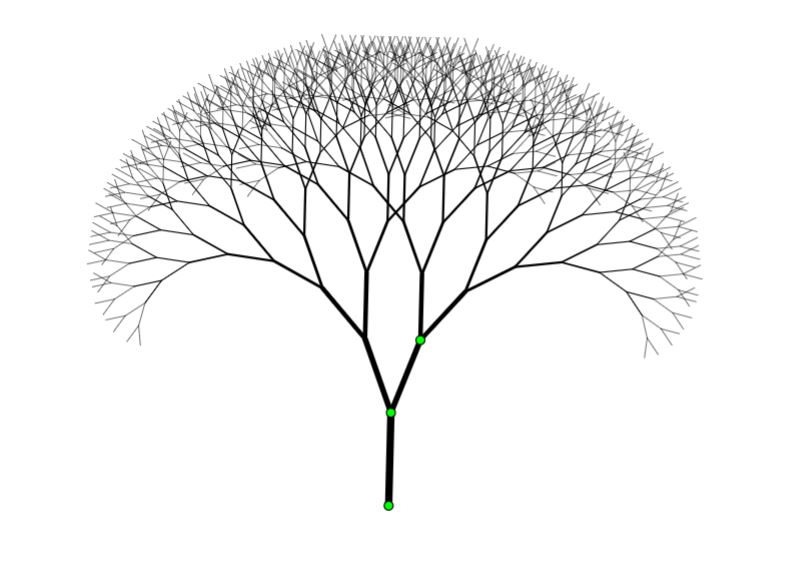
https://www.geogebra.org/m/tUD6vpFr#material/ypsveu3b
Determinismo o azar
La historia de la Ciencia es la historia de la búsqueda del orden dentro del caos. Newton con la Ley de Gravitación Universal había dado un paso de gigante en la búsqueda del orden en el universo.

Desde Newton y durante más de tres siglos los científicos de todas las disciplinas se han lanzado a la desenfrenada carrera de encontrar las leyes matemáticas que rigen el funcionamiento del Universo. Pensaban que el mundo es un gigantesco engranaje que funciona como un mecanismo de relojería.
carrera de encontrar las leyes matemáticas que rigen el funcionamiento del Universo. Pensaban que el mundo es un gigantesco engranaje que funciona como un mecanismo de relojería.
Las ecuaciones diferenciales podrán predecir el estado del sistema conociendo las condiciones iniciales del mismo. Los matemáticos del siglo XVIII recogieron el reto: los Bernouilli, Euler, d´Alembert, Lagrange y Laplace entre otros, se lanzaron a completar y explicar el universo newtoniano.
Pero estas ecuaciones que podían servir para sistemas simples son incapaces de predecir el estado de las partículas de gas encerradas en un globo, o de los miles de gotas que forman un torrente. No sirven para sistemas complejos formados por miles o millones de partículas.
predecir el estado de las partículas de gas encerradas en un globo, o de los miles de gotas que forman un torrente. No sirven para sistemas complejos formados por miles o millones de partículas.
A lo largo del siglo XIX los científicos resolvieron en parte esta dificultad mediante el análisis estadístico.
No podremos determinar el movimiento de todas y cada una de las partículas del torrente, pero al menos sabremos lo que hará este globalmente.
En la primera mitad del siglo XX coexistían estos dos paradigmas científicos: el determinista, con sus ecuaciones diferenciales para los sistemas simples y el estadístico para los sistemas complicados, con muchos grados de libertad en los que reina el azar.
Teoría del Caos
Un sistema dinámico es un conjunto de elementos que interactúan entre sí modificándose a través del tiempo. Las fronteras del sistema le separan del mundo exterior.
Hay infinidad de sistemas cuyo comportamiento se puede describir mediante ecuaciones lineales (un péndulo simple, una bola que cae, la trayectoria de un proyectil…). La evolución del sistema se puede predecir resolviendo esas ecuaciones. Y pequeños cambios en las condiciones iniciales producen pequeñas variaciones en el resultado final
Sin embargo, hay sistemas que son extremadamente sensibles a las pequeñas variaciones en las condiciones iniciales provocando cambios sustanciales en el resultado final. Son sistemas impredecibles, aunque no dependen del azar. Son los sistemas caóticos.


El universo está poblado de sistemas que se comportan de manera caótica. Las llamas de una hoguera, el humo, el agua en un arroyo, las olas del mar, la forma de un relámpago son manifestaciones cotidianas del caos. Todos ellos son fenómenos complejos.
Pero lo que nadie podía imaginar es que un sistema simple pudiese tener un comportamiento caótico. Un simple péndulo doble es un sistema caótico.
La extraña bifurcación de la función logística
La función f(x) = r·x·(1-x) con 0 < x < 1, y 0 < r < 4 rige el crecimiento de poblaciones en un entorno cerrado. Es una simple parábola.
El mecanismo es el siguiente.
Se parte de una población x0. Para un determinado valor de r (tasa de crecimiento), la población en un momento dado x n+1 se obtiene aplicando la fórmula al estado anterior x n
x n+1 = r·xn·(1-xn)
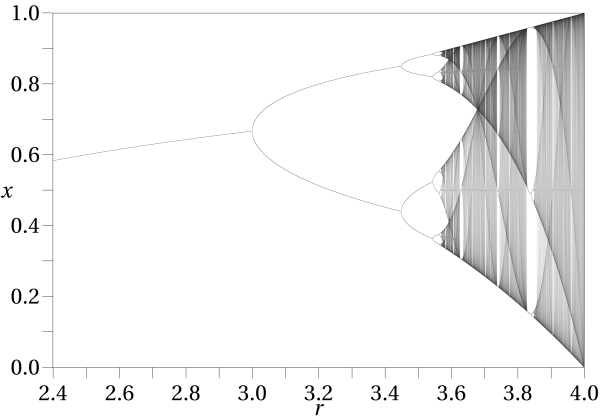
Para cada valor de r, la población al cabo del tiempo se estabiliza en un valor determinado de x. Y a pequeños cambios de ese valor de r le corresponden pequeñas variaciones de ese valor de x. Todo parece ir bien cuando r varía desde 0 hasta 3.
Pero a partir de r = 3 los valores de x se hacen inestables y parecen saltar de una unidad de tiempo a la siguiente oscilando entre dos valores distanciados para cambios muy pequeños de r. (0.5 y 0.8 para r = 3.2).
La gráfica se ha bifurcado en dos ramas. Más adelante se vuelve a bifurcar en 4 ramas y a partir de r = 3.57 parece que x no sigue ninguna pauta y puede tomar infinitos valores. Y no importa el valor inicial x0 que tomemos. Parece que el valor final de x es completamente aleatorio. Pero viene dado por la iteración de una simple función cuadrática:
f(x) = k·x·(1-x).


https://www.geogebra.org/m/fwahyxwp
https://www.geogebra.org/m/ugb6tpc7
Ha aparecido el caos.
La Mariposa de Lorenz
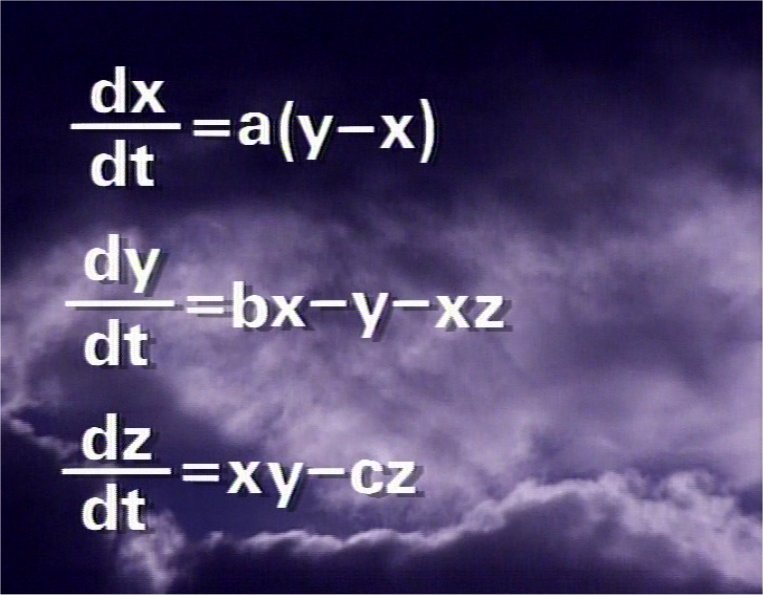 En 1960 Edward Norton Lorenz (1917-2008), matemático y meteorólogo estadounidense, pionero en el desarrollo de la llamada Teoría del Caos y conocido también por acuñar el conocido término efecto mariposa, desarrolló un modelo matemático para realizar previsiones del tiempo.
En 1960 Edward Norton Lorenz (1917-2008), matemático y meteorólogo estadounidense, pionero en el desarrollo de la llamada Teoría del Caos y conocido también por acuñar el conocido término efecto mariposa, desarrolló un modelo matemático para realizar previsiones del tiempo.
Este modelo era bastante simple y contemplaba sólo tres variables que rigen el movimiento de convección, relacionadas entre sí mediante tres ecuaciones diferenciales que ya se han hecho famosas.
Lorenz puso a trabajar su ordenador, en el que cada minuto simulaba el paso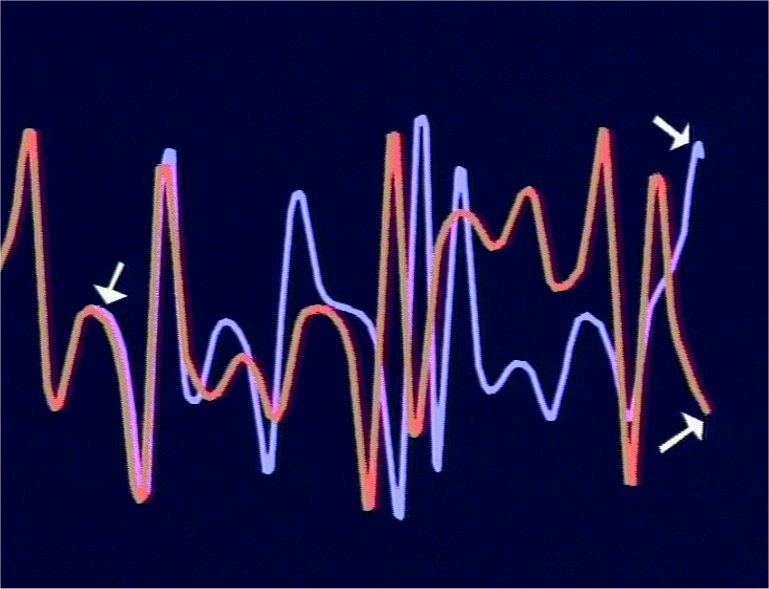 de un día. Con sorpresa
de un día. Con sorpresa
comprobó que una diferencia de menos de una milésima en las variables producía, al cabo de pocos minutos (unos días simulados), un estado climático totalmente distinto.
Había descubierto la segunda gran característica de los fenómenos caóticos: una pequeña variación de las condiciones iniciales produce grandes cambios en el sistema a lo largo del tiempo.
Es lo que se conoce como efecto mariposa.

Los valores de las tres variables representaban el estado del sistema en un instante dado. Lorenz asoció estos tres valores con las coordenadas de un punto en un espacio tridimensional. La secuencia de puntos trazaba una trayectoria continua y permitía ver la evolución del sistema. Si el sistema alcanzase un estado estable la curva se detendría en un punto; si fuese un sistema periódico describiría una circunferencia.
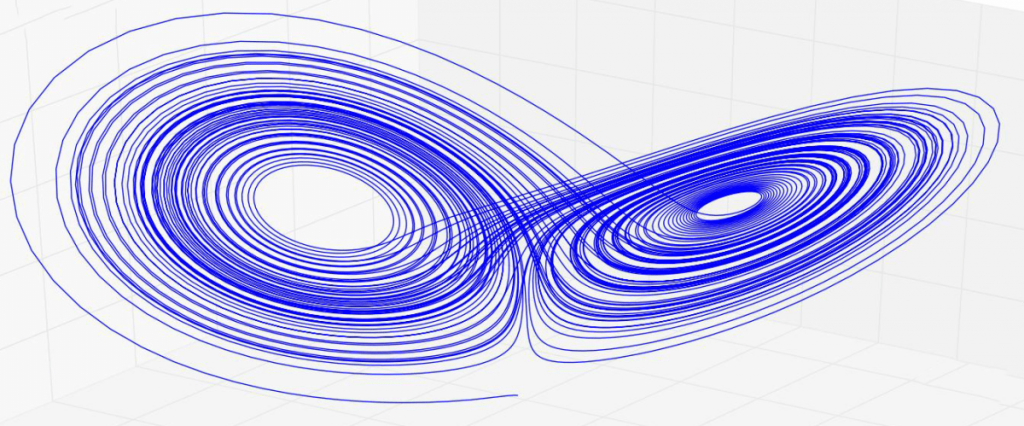
Sin embargo, la trayectoria manifestó una gran complejidad. Dibujó una extraña curva en el espacio que se parecía a una hélice doble en tres dimensiones cuyos puntos nunca se repetían. A pesar de ello había regiones que actuaban como extraños atractores. La figura se asemejaba a una mariposa con las alas extendidas. Desde entonces se conoce como el atractor de Lorenz.
La mariposa de Lorenz era el primer retrato en 3D de un sistema caótico.

Los matemáticos no le hicieron mucho caso, pero en él estaba el germen de la Teoría del Caos.
Fractales y caos
En su nacimiento allá por los años 70 del pasado siglo XX, el caos y los fractales no parecían estar relacionados. Pero los dos son hermanos matemáticos: ambos buscan la estructura profunda de la irregularidad.
En los dos la imaginación geométrica es lo más importante. En pocas palabras, los fractales nos presentan un nuevo lenguaje con el que describir algunas de las formas del caos, la cara más frecuente de la Naturaleza.

Definitivamente la geometría de la naturaleza tiene una cara fractal.Muchos fenómenos y formas naturales tienen en su estructura profunda el principio de autosimilitud. Esto permite utilizar la geometría fractal para explicar y predecir con base matemática muchos fenómenos complejos desde la evolución del cambio climático, o el estudio de fenómenos geológicos para predecir terremotos, hasta la respuesta del desarrollo de un tumor ante un tratamiento médico o el estudio del ritmo cardiaco para evitar el síndrome de la muerte súbita.
Actividades
Bibliografía
Geometría fractal
- GUZMÁN, M; MARTÍN, M.A.; MORÁN, M y REYES, M. Estructuras fractales. Editorial Labor. Madrid. 1993
- MANDELBROT, Benoît. La geometría fractal de la naturaleza. Tusquets Editores. Colección Metatemas. Barcelona 1997.
- MANDELBROT, Benoît. Los objetos fractales. Forma, azar y dimensión. Tusquets Editores. Colección Metatemas. Barcelona 1997.
- MANDELBROT, Benoît. El fractalista. Memorias de un científico inconformista. Tusquets Editores. Colección Metatemas. Barcelona 2014.
- PÉREZ SANZ, Antonio. Más por menos. Entender las matemáticas. Editorial Espasa y RTVE. Madrid 2011.
- STEWART, Ian. ¿Juega Dios a los dados?Crítica, Barcelona 1991.
- STEWART, Ian.De aquí al infinito. Crítica, Grijalbo Mondadori, S.A., Barcelona 1998.
Teoría del Caos
- GLEIK, J.: Caos. Seix Barral. Barcelona, 1988.
- LORENZ, E. Deterministic nonperiodic flow.Journal of the Atmospheric Sciences, nº 20. 1963. Pág 130-141
- PEITGEN, H. O.; JÜRGENS, H Y SAUPE, D. Chaos and Fractals. Springer-Verlag, New York 1992.
- MARTÍN, M.A.; MORÁN, M y REYES, M.: Iniciación al Caos. Editorial Síntesis. Madrid. 1995.
- PETERSON, I.: El turista matemático. Alianza Editorial. Madrid, 1992
- SPARROW, C. The Lorenz Equations: Bifurcations, Chaos and Strange Attractors. Springer. New York, 1982.
Vídeos
Programa de rtve ‘Más por menos: fractales, la geometría del caos’