Casarse en Machuria
En un territorio llamado Machuria (no por casualidad, y no situado en un territorio concreto, sino bastante extendido en el tiempo y en el espacio: el machismo), cuando una chica quería casarse tenía que pedir permiso. Iba junto con el chico con el que se había prometido al palacio del ‘jefe’ y este ponía en la mano cerrada de la chica seis trozos de igual longitud de una cuerda fina que sobresalían por los dos lados de su mano; su pretendiente tenía que ir uniéndolos (haciendo nudos) de dos en dos por cada lado de la mano sin que la chica la abriera, para no poder saber los extremos de cada una; cuando estaban hechos los seis nudos la chica abría la mano: si la cuerda salía formando un anillo podían casarse; si no tenían que postergar la boda.
Podían recurrir a una nueva oportunidad igual pasado un año; si esta también era negativa ya no había más oportunidades: no tenían derecho a casarse. ¿Podemos evaluar lo difícil que era casarse en Machuria?
Casarse en Remachuria
Remachuria, territorio cercano a Machuria, tenía un caid todavía más reaccionario que allí, que quería endurecer las condiciones de casamiento respecto a Machuria: aplicaría el mismo procedimiento pero, en vez de con seis, con ocho trozos de cuerda fina.
¿Crees que es más difícil casarse en Remachuria que en Machuria? ¿Cuál es la probabilidad en Remachuria?
SOLUCIONES
Machuria.- Parece que el ‘jefe’ del territorio no era muy amigo de los matrimonios entre sus súbditos, porque la probabilidad de que salga un anillo parece ‘evidente’ que es muy pequeña. Pero puede pasar, como muchas otras veces en asuntos relacionados con el azar, que las apariencias engañen.
Vamos a hallar la probabilidad del primer año calculando los casos favorables (CF) y los posibles (CP). Atamos como queramos las cuerdas que salen por uno de los lados de la mano, porque no supone ninguna limitación de lo que sucederá al atar por el otro lado, y es en ese lado donde nos fijamos. Las maneras posibles de atar son las siguientes: en el primer nudo, elegido uno de los extremos lo podremos atar con cualquiera de los otros cinco (5 por tanto); hecho ese primer nudo, elegimos el segundo extremo, para lo que ya solo hay tres para elegir; y atado el segundo nudo ya solo nos quedan dos extremos sueltos y la única posibilidad de elección es atarlos entre sí. Por tanto CP = 5x3x1 = 15.
¿En cuántos de esos casos sale un único anillo? Esos serán los CF. Elegido uno de los extremos, el primer nudo podemos hacerlo con todas las cuerdas excepto con aquella que ya está unida por arriba con ella: cuatro posibilidades; para el segundo nudo tenemos que evitar la cuerda que ya está unida por arriba con ella, dos casos; en el tercero solo quedan dos extremos, luego una sola opción. Con todo eso CF = 4x2x1= 8.
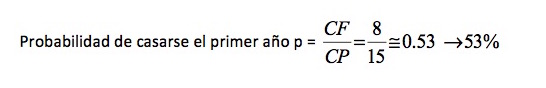
Un resultado sorprendente: el primer intento es positivo en más de la mitad de los casos.
Miramos ahora el conjunto de los dos años. La probabilidad de que no salga el anillo en un año es
(1 – p) = 1 – 0.53 = 0.47;
la de que no salga ninguno de los dos años, (que no salga en ninguna de los dos intentos), es el producto de sus probabilidades:
(1-p)x(1-p) = 0.47×0.47 = 0.22.
Eso indica que haciendo la prueba dos años seguidos hay una probabilidad del 22% aproximadamente de que no salga un solo anillo ninguno de los dos, que serán las parejas que no se podrán casar. Es decir que podrán casarse, todos los demás: el 78% de los que lo intenten dos años.
La probabilidad de casarse en el segundo año puede verse de otra manera. La probabilidad de hacer un solo anillo en el segundo intento volverá a ser del 53%, pero considerando solo al 47% que no acertó el primer año, que son los únicos que repetirán la prueba. Como 0.53×0.47 @ 0.25, se tiene que el segundo año consigue el anillo el 25% de las parejas que se habían presentado; luego solo hay un 47% – 25% = 22% que no se podrá casar
Mirándolo de cualquiera de las dos formas, y contra lo que parecía ‘evidente’,
¡no es muy difícil casarse en Machuria!
Remachuria.- Por la misma razón que en Machuria, la probabilidad el primer año, será
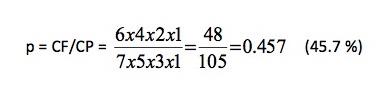
En dos años seguidos, la probabilidad de que ninguno salga es
(1-p)x(1-p) = 0.284 (28.4%)
Lo que quiere decir que el 71.6% sí que podían casarse. ¡El caid de Remachuria era bruto pero no muy espabilado con la probabilidad!
[Puede verse una versión en video del problema ‘Casarse en Machuria’ en este enlace y de su solución en este otro].




