DESCARREGA EL PDF DESCARGA EL PDF català DESCARGA O PDF galego
Autor: Manuel de León Rodríguez
Aplicaciones interactivas: José Luís Álvarez García y Javier Cayetano Rodríguez
Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)
CONTENIDO
- El hueso de Ishango.
- El origen de nuestros números.
- Pitágoras. El nacimiento de la Aritmética.
- ¿Cuántos números primos hay?
- El gran reto: la distribución de los números primos.
- Los descubrimientos de Fermat.
- El teorema de los números primos de Gauss.
- La hipótesis de Riemann.
- Los primos de Mersenne y los cazadores matemáticos de fantasmas.
- ¿Por qué es importante conocer más y más números primos?
- Aritmética modular.
- ¿Cómo funciona la encriptación con números primos?
- Misterios y conjeturas por demostrar sobre números primos: Primos gemelos. Conjeturas de Goldbach
- Ordenadores y números primos.
- Bibliografía
Contar fue la primera actividad matemática desarrollada por el ser humano: los días, las cabezas de ganado, los miembros de la tribu. E inmediatamente surge la necesidad de registrar los datos.
El hueso de Ishango
Hace más de 20.000 años, unos hombres o mujeres tallaron una serie de muescas en un peroné de un babuino en Ishango, en el lago Eduardo, cerca del nacimiento del Nilo. Esas columnas de muescas representan cantidades que nos han intrigado desde hace más de 50 años tras su descubrimiento.

El origen de nuestros números
Contar nos ha llevado a la invención de los números, uno de nuestros mayores logros. Nuestros números nacen en India, y los árabes los traen a Europa en el siglo X. Los números del 9 al 1, tal y como los representamos hoy en día, aparecen por primera vez en España, en el Codex Vigilanus o Codex Albeldensis, compuesto por el monje Vigila en el siglo X en la Rioja. El cero causa una revolución cuando Fibonacci (Leonardo de Pisa) lo introduce en Europa en el siglo XII, en su Liber abaci (Libro del ábaco); Fibonacci lo aprendió de los árabes en sus viajes acompañando a su padre por el norte de África. El nuevo sistema decimal, con el cero incluido, simplificaba de una manera casi mágica los cálculos de los comerciantes, acostumbrados al ábaco, que no precisa del cero. La lucha entre ambos sistemas fue tremenda, y el cero fue acusado de elemento demoníaco.
Codex Albeldensis, compuesto por el monje Vigila en el siglo X en la Rioja. El cero causa una revolución cuando Fibonacci (Leonardo de Pisa) lo introduce en Europa en el siglo XII, en su Liber abaci (Libro del ábaco); Fibonacci lo aprendió de los árabes en sus viajes acompañando a su padre por el norte de África. El nuevo sistema decimal, con el cero incluido, simplificaba de una manera casi mágica los cálculos de los comerciantes, acostumbrados al ábaco, que no precisa del cero. La lucha entre ambos sistemas fue tremenda, y el cero fue acusado de elemento demoníaco.
Pitágoras. El nacimiento de la Aritmética
Todas las cosas que pueden ser conocidas tienen número; pues no es posible que sin número nada pueda ser conocido ni concebido
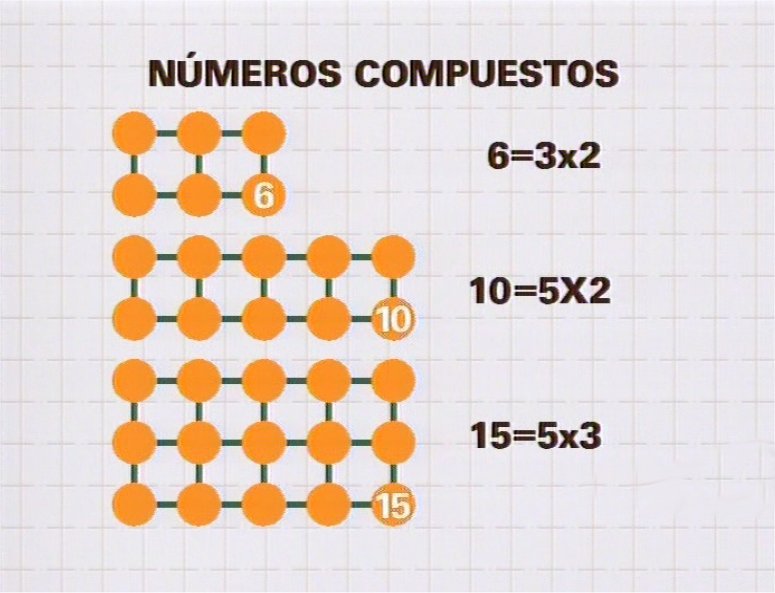
Un número es compuesto cuando tiene divisores distintos de él mismo y de la unidad, es decir cuando se puede dibujar como un rectángulo numérico.
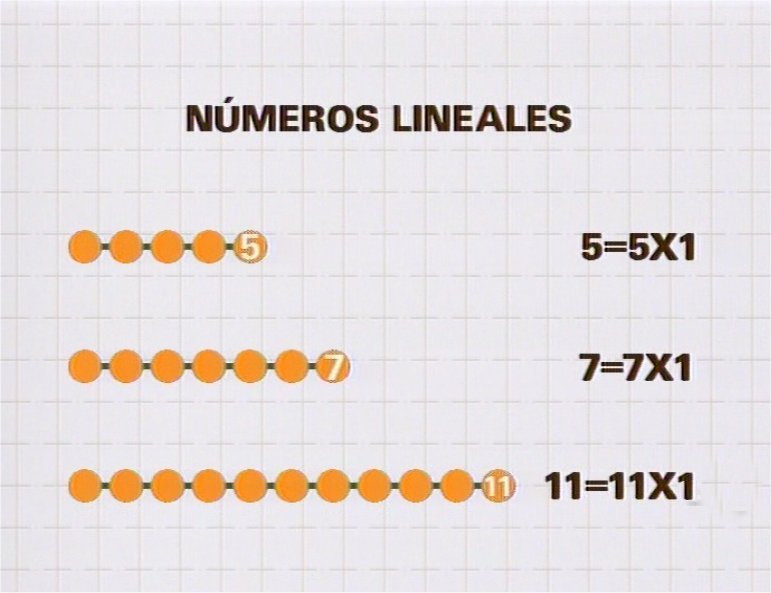
Un número es primo cuando sólo es divisible por la unidad y por él mismo. No se puede representar mediante un rectángulo. También se denominaba número lineal. Los números 2, 3, 5, 7, 11… son primos
¿Cuántos números primos hay?
Supongamos que solo hay un número finito de números primos
![]()
consideramos el número
![]()
Entonces, q es un nuevo número primo, ya que ninguno de los primos puede ser divisor de q. Llegamos a una contradicción. Esta es una prueba por reducción al absurdo . Hay infinitos.
Pero no se conoce un patrón que nos diga cómo están distribuidos dentro del conjunto de los números naturales.
El gran reto: la distribución de los números primos
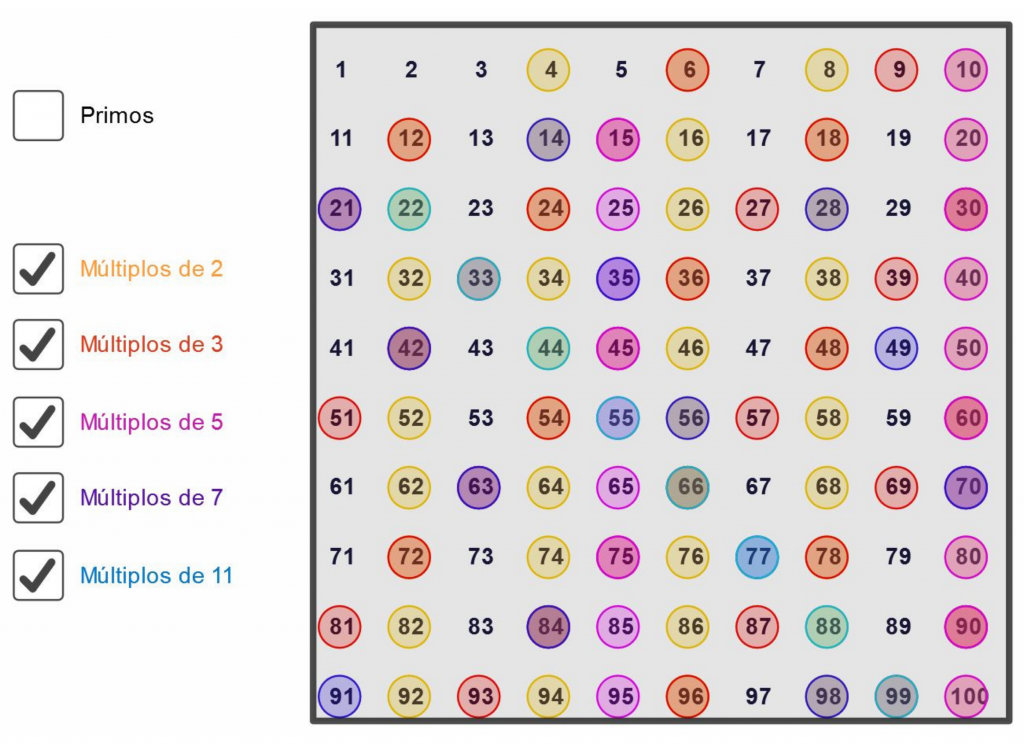
La Criba de Eratóstenes es un procedimiento para determinar todos los números primos hasta cierto número natural dado.
Esto se hace recorriendo una tabla de números usando el siguiente procedimiento. Si queremos conocer los primos entre 1 y 100, comenzamos por el 2 y tachamos sus múltiplos, luego el 3 y sus múltiplos, así hasta que sea posible; los números que quedan son primos. Eratóstenes de Cirene fue un matemático griego famoso por haber calculado la longitud de la circunferencia de la Tierra.
Desde entonces muchos matemáticos se han preguntado cómo estarán distribuidos los números primos dentro del conjunto de los números naturales. Matemáticos tan notables como Fermat, Gauss, los Bernoulli, Euler y Riemann han contribuido a aclarar esta distribución mediante resultados que en muchos casos todavía no han podido ser demostrados y que por tanto son meras conjeturas matemáticas.
El mismo Euler afirmaba en 1751:
Descubrir algún orden en la progresión de los números primos es un misterio que el espíritu humano no penetrará nunca
Los descubrimientos de Fermat
Fermat descubrió que hay dos grandes familias de números primos:
– Unos son de la forma 4 n + 1: 5, 13, 17, 29, 37, 41…
– Los otros de la forma 4 n + 3: 3, 7, 11, 19, 23, 31, 43…
También descubrió que todos los de la primera familia se pueden escribir como la suma de dos cuadrados.
Pero en cambio, ninguno, de los de la segunda familia se puede descomponer en la suma de dos cuadrados.
El Teorema de los números primos de Gauss
Los números primos no se distribuyen de manera uniforme entre los números naturales, de hecho son cada vez más raros según vamos considerando números más grandes; entre 0 y 1000  hay 168, entre 10.000 y 11.000 hay 106 (62 menos), entre 100.000 y 101.000 hay sólo 81. Según avanzamos en los números naturales los primos empiezan a escasear.
hay 168, entre 10.000 y 11.000 hay 106 (62 menos), entre 100.000 y 101.000 hay sólo 81. Según avanzamos en los números naturales los primos empiezan a escasear.
Ante este hecho, Gauss formuló la hipótesis, de que la cantidad de números primos menores que un número x tiende al cociente entre el número y su logaritmo neperiano. De hecho, cuando contaba sólo 14 años dejo entre sus apuntes esta anotación:
números primos menores que a ( = ∞) a / l a
Si llamamos π(x) al número de primos menores que x, el teorema de los números primos, enunciado por Gauss, afirma que
![]() O lo que es lo mismo, la fórmula que proporciona la cantidad de primos menores que un número n dado es
O lo que es lo mismo, la fórmula que proporciona la cantidad de primos menores que un número n dado es
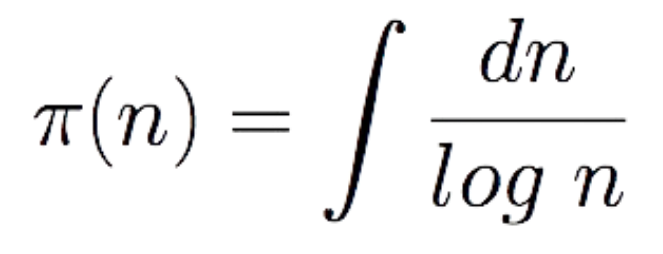
Gauss conjeturó el patrón pero no pudo demostrarlo. Al fin el teorema de los números primos fue demostrado por Jacques Hadamard (1865-1963) y C. J. de la Vallée Poussin (1866-1962) en 1896. Este resultado nos permite aventurar que entre los mil números que siguen al número 100.000.000 haya, aproximadamente, unos 52 primos.
La hipótesis de Riemann
La hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función zeta de Riemann ζ(s)
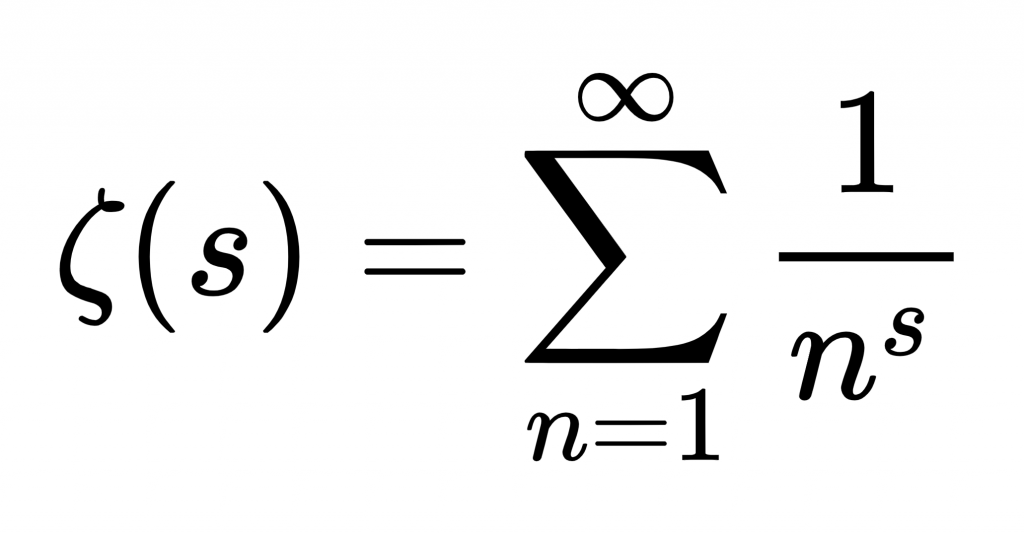
La hipótesis afirma que la parte real de todo cero no trivial de la función zeta de Riemann es ½.

Demostrarla nos permitiría descubrir la distribución que siguen los números primos.
Es una de las conjeturas abiertas más relevantes y uno de los Siete Problemas del Milenio de la Fundación Clay.
Los primos de Mersenne y cazadores matemáticos de fantasmas
Saber si un número es primo o no es fácil para números pequeños, pero puede ser una tarea ardua o casi imposible para números muy grandes.
Un primo de Mersenne es un número de la forma 2p -1, donde p también es un número primo.
Marin Mersenne (1588 –1648) fue un sacerdote, matemático y filósofo francés del siglo XVII, muy activo en su época comunicando entre sí y con él a los intelectuales europeos
Hasta ahora solo se conocen 51 primos de Mersenne, y de ellos, 282.589.933 – 1 es el mayor número primo conocido, con 24.862.048 dígitos.
Actualmente existe una red de “cazadores de números primos”, la Great Internet Mersenne Prime Search (GIMPS) que busca primos nuevos desde 1996.
¿Por qué es importante conocer más y más números primos?
Un problema es transmitir la clave al destinatario. Se habla de encriptación simétrica cuando la clave para encriptar es la misma que
para desencriptar; en otro caso, se dice asimétrica. Esto es lo que pasa con las claves basadas en la descomposición de un número en sus factores primos. Encriptar es transformar un mensaje en otro que solo nosotros y nuestro destinatario somos capaces de descifrar. Para ello, tenemos que conocer la clave. Como todo mensaje se puede traducir en números, reducimos el problema a transmitir números. Si conocemos dos primos muy grandes y los multiplicamos, obtendremos un número enorme. Si transmitimos ese número, nadie será capaz de descomponerlo en sus factores originales.
En 1978, Ted Rivest, Adi Shamir y Leonard Adleman, inventaron el algoritmo RSA (llamado así por sus iniciales) y que usa este procedimiento.
Aritmética modular
La aritmética modular se basa en la idea de números congruentes.
Dos números enteros a y b son congruentes módulo n, si ambos dejan el mismo resto al dividirlos por n, o, o lo que es lo mismo, si a − b es un múltiplo de n.
Se conoce también como “aritmética del reloj”, ya que superado el módulo, vuelven a repetirse las clases de congruencia. Por ejemplo 5 y 17 son congruentes módulo 12, por eso las 17 horas son las 5 de la tarde.
La aritmética modular fue introducida en 1801 por Carl Friedrich Gauss en su libro Disquisitiones Arithmeticae.
¿Cómo funciona la encriptación con números primos?
- Se eligen dos números, p y q, y se multiplican, n = p · q.
- Se calcula este número z = (p-1) · (q-1).
- Se elige un número primo k, tal que k sea coprimo (sin divisores comunes) con z.
- La clave pública es el par (n,k).
- La clave privada es un número j tal que k · j = 1, (mod z).
- El mensaje convertido en un número P lo ciframos usando esta ecuación Pk = E (mod n).
- Enviamos E. El destinatario conoce la clave privada, j, y hace el siguiente cálculo, Ej = P (mod n). (Ver ejemplo en Criptografía RSA… los Números Primos nos protegen)

La razón de que funcione está en el llamado teorema teorema de Euler-Fermat.
Si a y n son enteros coprimos, entonces
aψ(n) ≡ 1 (mod n),
donde ψ(n) es la llamada función de Euler (es el número de enteros positivos menores o iguales a n y coprimos con n).
Misterios y conjeturas por demostrar sobre números primos
Primos gemelos
Solamente hay dos números primos consecutivos: 2 y 3. ¿Sabrías justificar por qué no puede haber otros dos números primos consecutivos?
Pero hay un gran número de pares de números primos que difieren en dos unidades, por ejemplo: 3 y 5, 5 y 7, 11 y 13, 17 y 19, … Cuando dos números primos se diferencian en dos unidades, como los anteriores, se les llama «primos gemelos». En esta aplicación puedes buscar alguno más y descubrir algunas interesantes propiedades de estas parejas de primos gemelos.¿Cuántas parejas de primos gemelos hay? ¿Habrá infinitas parejas?Aún no lo sabemos. Es uno de los retos por descubrir de los números primos. Pero hay más, y con mucha historia detrás.
Conjeturas de Goldbach
Muchas otras conjeturas no demostradas pueblan el universo en torno a los números primos. Las más populares se deben al matemático prusiano Christian Goldbach (1690-1764).
Conjetura fuerte
Todo número par, mayor que 2, es la suma de dos números primos.
4 = 2+2 6=3+3 8=3+5
10=3+7… 32=13+19… 48=7+41
Conjetura débil
Todo número impar mayor que 5 se puede expresar como suma de tres números primos.
7 = 2+2+3 9 = 3+3+3 11 = 3+3+5
13 = 3+5+5 25 = 5+7+13 33 = 5+11+17
La conjetura débil fue demostrada en 2013, tras más de 270 años de esfuerzos de los matemáticos de todas las épocas, por el matemático peruano, afincado en Francia, Harald Helfgott.
Desde 1742, año en que Goldbach le escribió sus sospechas a Euler, nadie ha conseguido demostrar que la conjetura fuerte sea cierta. Por otra parte, tampoco nadie ha encontrado ningún número que la desmienta.
Las investigaciones realizadas con ordenadores han probado que la conjetura es cierta para los primeros millones de números, pero esto no significa que lo sea para todos.
Ordenadores y números primos
Los ordenadores han contribuido a hacer un poco de luz sobre algunos de los misterios de los números primos. De hecho, los números primos se usan también para evaluar el rendimiento bruto de los modernos procesadores y permiten saber si estos chips son capaces de soportar cargas de trabajo muy elevadas durante largos periodos de tiempo.

Bibliografía
CILLERUELO, J. y CÓRDOBA, A. Los números. CSIC-Ed. Catarata. Madrid 2010
GONZÁLEZ URBANEJA, P.M. Pitágoras. El filósofo del número. Ed. Nivola. Colección La matemática en sus personajes. Madrid 2001.
GONZÁLEZ VASCO, M. I. Las matemáticas de la criptología. Secretos demostrables y demostraciones secretas. Ed. Catarata. Colección Miradas matemáticas. Madrid 2018
MUÑOZ CASADO, J.L. Riemann. Una visión nueva de la geometría. Ed. Nivola. Colección La matemática en sus personajes. Madrid 2001.
SÁNCHEZ FERNÁNDEZ, C. y ROLDÁN INGUANZO, R. Goldbach. Una conjetura indomable. Ed. Nivola. Colección La matemática en sus personajes. Madrid 2006.
SAUTOY, MARCUS de. La música de los números primos. Acantilado. Barcelona, 2007.
Video
PÉREZ SANZ, A. Números naturales, números primos. Serie Más por menos. RTVE.