Estadística y mucho más: Matemáticas frente al Covid19

DESCARGA EL PDF castellano  DESCARGA O PDF galego

Autor: Fernando Corbalán, Gerardo Sanz, Santiago García Cremades

Aplicaciones interactivas: Manuel Sada

Locuciones: César Goldi (voz); Juanjo Fernández (Grabación y efectos sonoros)

CONTENIDO

1. 1. 1. 1. John Snow y la causa del cólera
         2. Las vacunas
         3. Incertidumbres
         4. El reino del azar. Casarse en Machuria
         5. El problema de los abrigos
         6. El covid y la matemática
         7. Modelos matemáticos aplicados a epidemiología
         8. Cuestiones relevantes a tener en cuenta en cualquier modelo
         9. Más sobre John Snow y la causa del cólera
         10. Más sobre Casarse en Machuria
         11. Andar borracho
         12. Preguntas inconvenientes
         13. Respuestas preguntas comprometidas
         14. Preguntas comprometidas (Respuestas más sofisticadas)
         15. Práctica

John Snow y la causa del cólera

Londres a mitad del siglo XIX era el centro industrial del mundo pero a la vez estaba azotado por epidemias derivadas de las miserables condiciones de vida de los trabajadores. La explicación aceptada en la época de la causa de las epidemias era la ‘teoría de las miasmas’: las enfermedades como el cólera eran causadas por unos malos aires que las transmitían.

John Snow (1813-58), un joven pero prestigioso médico establecido en el céntrico barrio del Soho encontró la relación entre el cólera y la falta de higiene, aunque para ello se tuvo que enfrentar a las ideas dominantes en la época y a pesar de que logró establecer el origen de los brotes de cólera en las fuentes, no fue reconocida su aportación hasta después de su temprana muerte.

La población se amontonaba en viviendas sin condiciones de habitabilidad, y además, al no haber un sistema de alcantarillado completo, se iban arrojando los desechos a la calle o al río Támesis.

Para más información

Las vacunas

Ha habido grandes logros recientes de lucha contra enfermedades como la polio (vacunas de Salk o Savin, 1956), con Elvis Preley vacunándose como reclamo [Fotos ELVIS1 o ELVIS2], la erradicación de la viruela (a partir de la acción conjunta de la OMS, la URSS y USA, desde 1958, que culminó en 1979) o la erradicación de la peste porcina (en 2011).

Incertidumbres

A la humanidad le ha costado mucho esfuerzo entender y saber manejarse con las incertidumbres.

Aquí encontrarás una historia sucinta de esta lucha y algunas situaciones para poder entrenar el estudio de situaciones de azar.

El reino del Azar. Casarse en Machuria

En un territorio imaginario llamado Machuria cuando una chica quería casarse tenía que pedir permiso. Iba junto con el chico con el que se había prometido al palacio del rey y este ponía en la mano cerrada de la chica seis trozos de igual longitud de una cuerda fina que sobresalían por los dos lados de su mano; su pretendiente tenía que ir uniéndolos (haciendo nudos) de dos en dos por cada lado de la mano sin que la chica la abriera, para no poder saber los extremos de cada una; cuando estaban hechos los seis nudos la chica abría la mano: si la cuerda salía formando un anillo podían casarse; si no tenían que postergar la boda.

Podían recurrir a una nueva oportunidad igual pasado un año; si esta también era negativa ya no había más oportunidades: no tenían derecho a casarse. ¿Podemos evaluar lo difícil que era casarse en Machuria?

Para más información

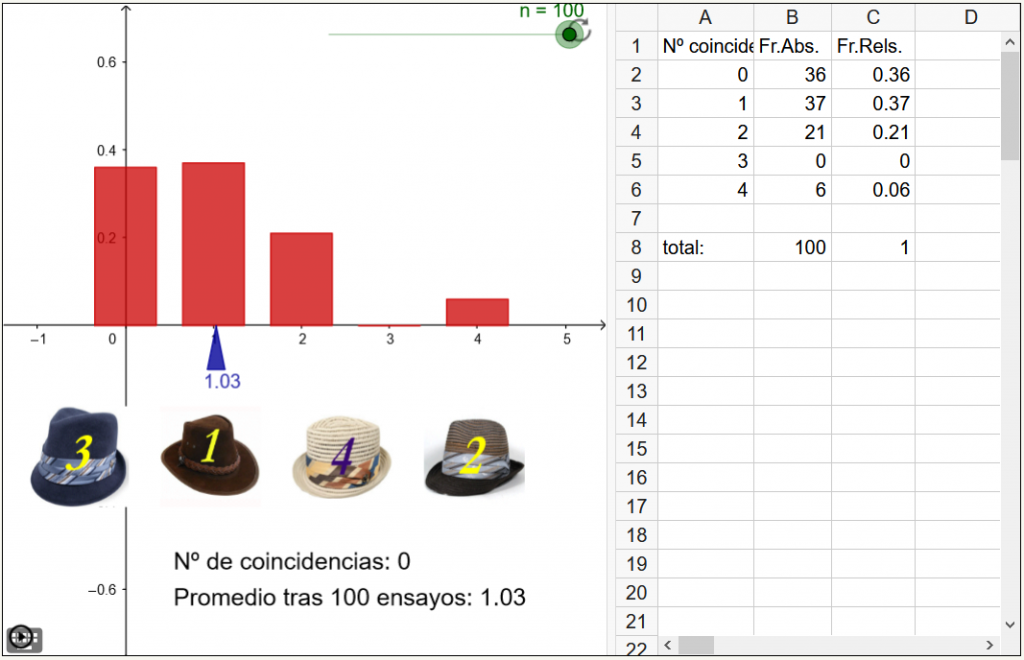
Problema de los abrigos

Un grupo de N personas van a una fiesta y al entrar dejan sus abrigos cada uno en una percha. Por desgracia la fiesta acaba bruscamente debido a un apagón de luz que dura demasiado tiempo. Al salir, como no hay luz, cada uno cogerá uno cualquiera y se irá a su casa. ¿Qué probabilidad hay de que ninguno de los asistentes escoja su abrigo?

Euler ya planteó este problema con sombreros.

Cuando nuestra sociedad pensaba que, aun con dificultades, éramos casi intocables, un virus ha venido a demostrarnos que somos mucho más vulnerables de lo que creíamos.

El covid y las matemáticas

Las matemáticas nos están ayudando a dar certezas en un mar de incertidumbre pandémica. Nuestro desconocimiento de los diferentes mecanismos de propagación de enfermedades junto al comportamiento del ser humano ha hecho que los modelos probabilístico-estadísticos sean una herramienta esencial en su estudio.

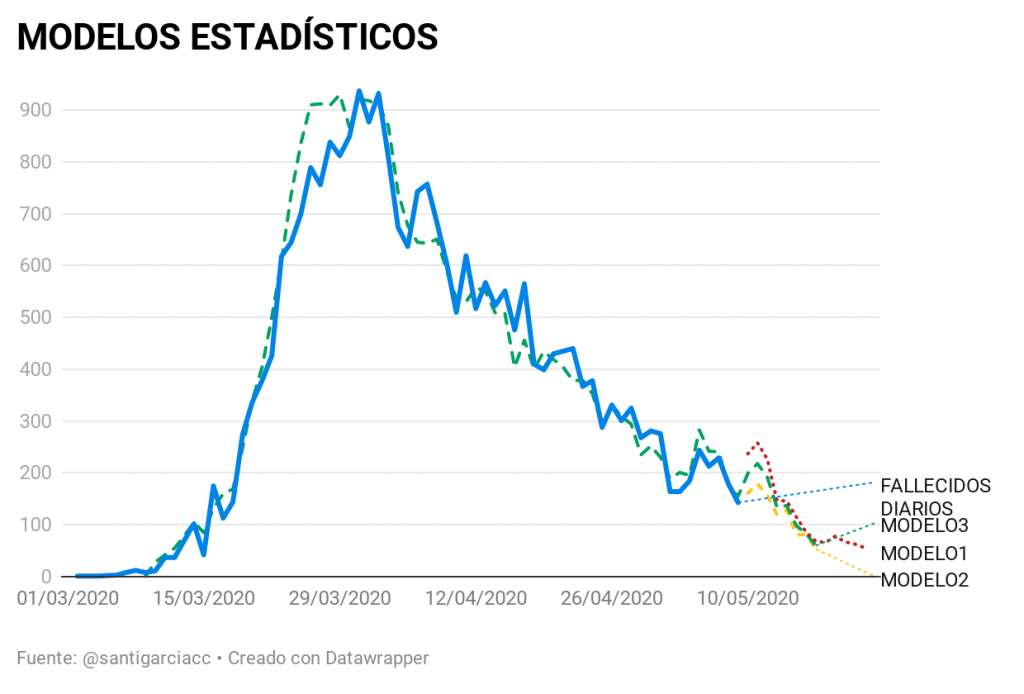
Cuando se tienen datos cambiando en el tiempo se recurre a las series temporales. El comienzo del uso de estas técnicas se sitúa en crack del 29, con George Udny Yule. Saber cómo evoluciona una variable que se ve afectada por cientos de otras variables tomó una gran importancia en economía, dando origen a la econometría.

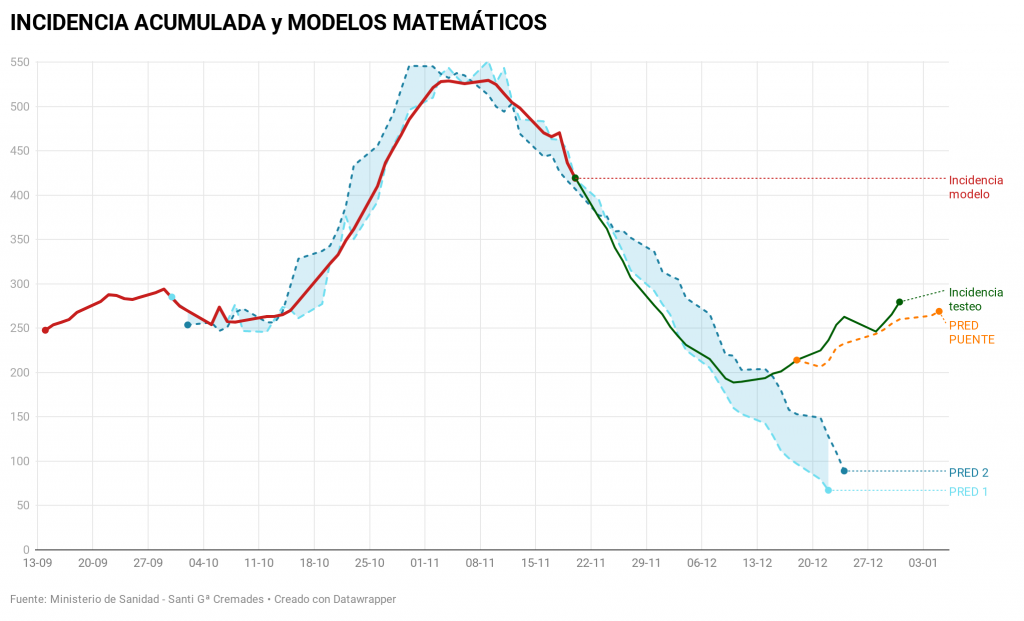
En estos modelos se pueden aplicar decenas de versiones: aditivos, multiplicativos, autorregresivos, con distintas frecuencias, etc. Desde el principio de la pandemia Santiago Gracía Cremades, de la universidad de Elche, desarrolló un modelo utilizado para predecir la curva de fallecidos de abril a mediados de mayo (figura 1) y la curva de la Incidencia Acumulada desde julio a diciembre (figura 2), con mejor aproximación que la mayoría de métodos.

Modelos matemáticos aplicados a la epidemiología

El modelo SIR fue el primero en levantar la mano, por razones evidentes, es el modelo que distribuye una población en tres categorías: Susceptibles, Infectados y Recuperados. Es un modelo basado en ecuaciones con derivadas, propuesto en 1926 por el escocés Anderson Gray McKendrick para estudiar la malaria.

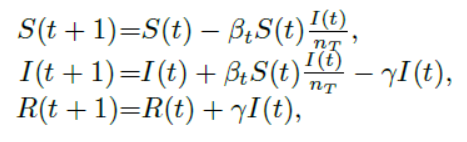
Desde entonces, cualquier estudio epidemiológico recurre a este modelo y un valor en concreto: el factor reproductivo del virus, conocido como Rt. Este parámetro indica la dinámica de la enfermedad y se considera la existencia de un brote cuando el valor es mayor que 1. En ese momento, la epidemia es susceptible de control.

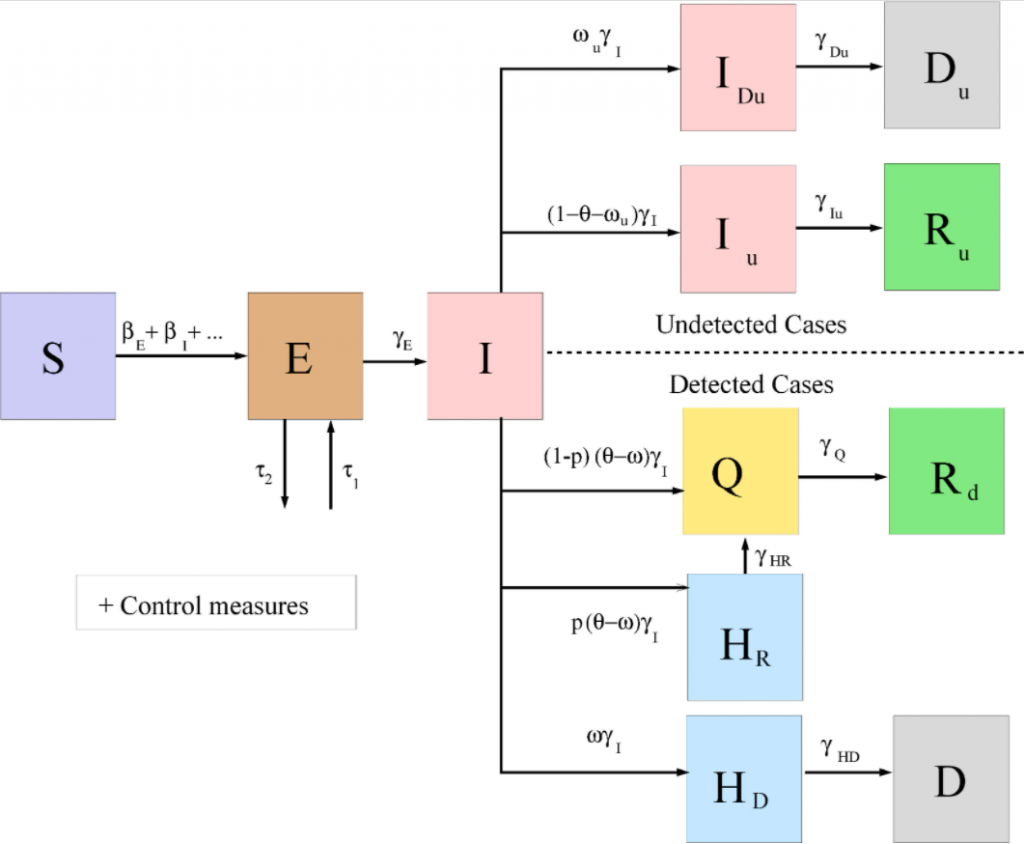
Hay muchas variantes, siendo el modelo SEIR (con la E de Expuestos) el más presente, donde se puede analizar a nivel teórico los efectos de las medidas restrictivas en el resto de variables. Este modelo tiene el problema evidente que si no tienes una buena estimación de los infectados, no obtenemos la información más relevante: cuánta gente puede estar inmunizada.

Puesto que en tiempo real el modelo SIR parecía tener sus debilidades, aparecieron nuevos modelos matemáticos, entre ellos, las cadenas de Markov, los modelos de supervivencia, los modelos de regresión y el machine learning, basado en Inteligencia Artificial.

Cuestiones relevantes a tener en cuenta en cualquier modelo

• Cuál es y cómo evoluciona la tasa de reproducción básica.
• Cómo afectan las restricciones administrativas a la evolución de la pandemia.
• Cómo afectan las restricciones de movilidad y otras medidas restrictivas.
• Cómo conocer la evolución futura del número de contagios, la llegada de nuevas olas o rebrotes y su comportamiento.
• ¿Qué características influyen más en que un paciente ingrese en un hospital? ¿Cómo predecir su evolución? ¿Cuál es la estancia media prevista? ¿Pasará a una UCI? ¿Cuál es la probabilidad de que sobreviva?
• Desarrollo de un modelo/herramienta que nos avise de un incremento significativo de casos.
• El comportamiento de la pandemia es diferente en distintos estratos de la población. La edad, el género y clase social parecen unos de los estratos de interés. ¿Hay otros? Cómo deben elaborarse los modelos predictivos teniendo en cuenta los estratos.

Más sobre John Snow y la causa del cólera

Hacia la mitad del siglo XIX Londres era el centro del mundo en muchos aspectos, en particular en el terreno industrial, pero era una ciudad sucia e insalubre, sobre todo para las clases trabajadoras. Basta recordar que del estudio de la misma surgió en 1848 el ‘Manifiesto comunista’ que llamaba a luchar por el cambio de la sociedad y a acabar con esas miserables condiciones de vida. La población se amontonaba en viviendas sin condiciones de habitabilidad, y además, al no haber un sistema de alcantarillado completo, se iban arrojando los desechos a la calle o al río Támesis.

Como consecuencia aparecían intermitentes pero continuados brotes de cólera, que causaban importantes números de muertes. John Snow (1813-58), un joven pero prestigioso médico establecido en el céntrico barrio del Soho encontró la relación entre el cólera y la falta de higiene, aunque para ello se tuvo que enfrentar a las ideas dominantes en la época y a pesar de que logró establecer el origen de los brotes de cólera, no fue reconocida su aportación hasta después de su temprana muerte. Como siempre luchar contra las ideas establecidas es complicado y con frecuencia no reconocido. John Snow (1813 –1858) desarrolló en toda su carrera un gran sentido de la observación: ya al realizar sus prácticas después de acabar sus estudios descubrió que la causa de las enfermedades que afectaban a los estudiantes de medicina era una intoxicación con los vapores de arsénico que se usaban para conservar cadáveres, con los que estaban en contacto al realizar autopsias. Y después fue un estudioso de los métodos para anestesiar, entonces en sus inicios, lo que le llevó incluso a asistir a la Reina en el alumbramiento de alguno de sus hijos.

Pero la relación de Snow con las epidemias y la determinación de la causa del cólera es su mayor contribución a la medicina. La explicación dominante y aceptada en esa época era la ‘teoría de las miasmas’: que las enfermedades infecciosas como el cólera eran causadas por unos malos aires que las transmitían. Pero en el caso del cólera, como lo que produce es disfunciones digestivas y no respiratorias, Snow pensó que esa teoría no servía. Más teniendo en cuenta que las zonas londinenses donde mayor incidía el cólera eran las del sur de la ciudad, donde el agua del abastecimiento, que venía del río Támesis, estaba más contaminada que en el norte. Y publicó un artículo en el que deducía que la causa de la enfermedad tenía que ser alguna sustancia presente en el agua, aunque fuera invisible al ojo humano, que producía unas diarreas severas.

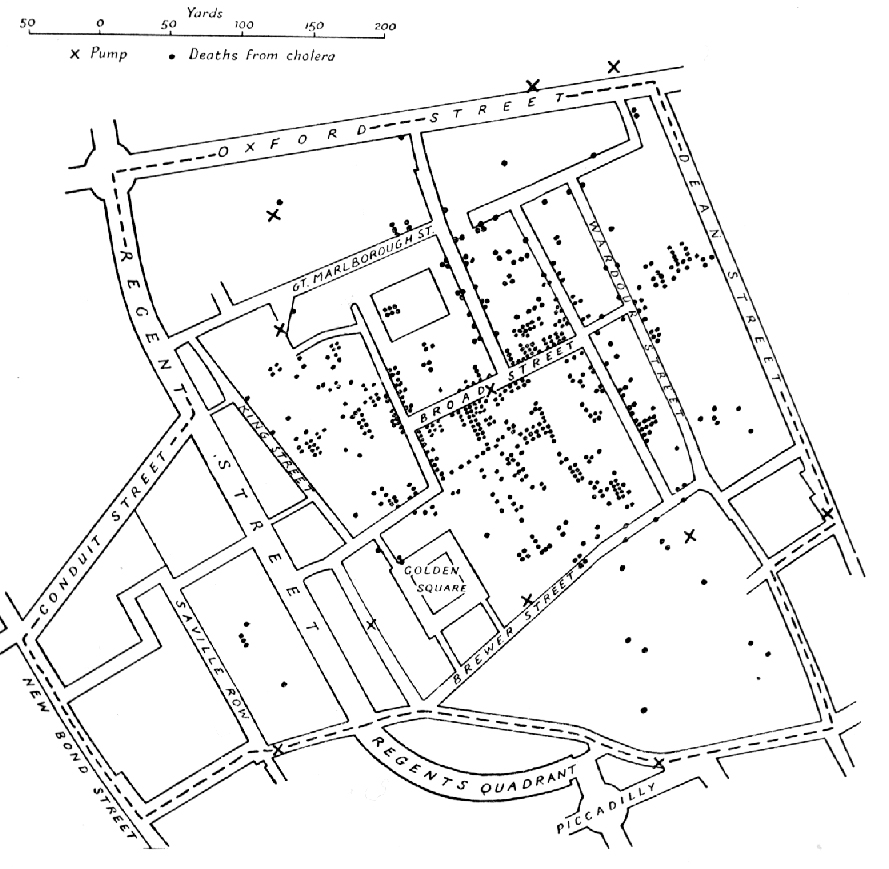
Una nueva epidemia de cólera en 1854 dio la oportunidad a John Snow de investigar de nuevo, hablando con los enfermos y sus familias, y los fue situando en el mapa de Londres, para tratar de encontrar una correlación con los lugares de los que los pacientes obtenían el agua para beber. Así identificó una bomba de agua contaminada en Broad Street como el origen del brote en el barrio del Soho, que al ser clausurada hizo bajar los casos de una manera importante. Añadía más claridad al origen el hecho de que entre los trabajadores de una cervecería cercana no hubiera ningún caso de cólera porque, por miedo a la enfermedad, solo bebían cerveza (que estaba fabricada con agua hervida). A pesar de todas las evidencias no logró que su teoría fuera aceptada, las teorías del miasma siguieron vigentes y la bomba volvió a abrirse al poco tiempo. Snow murió pronto y hubo que esperar a la siguiente epidemia de cólera (en 1866), cuando ya las autoridades comprobaron que las ideas de Snow eran correctas y que el agua de esa bomba venía mezclada con aguas fecales; y poco después, en 1884 Robert Koch finalmente identificó la bacteria causante del cólera.

Pero aunque tarde, hoy en Londres se reconoce la aportación de John Snow, porque en la misma calle londinense continua una reproducción de la misma bomba de agua, con una placa que recuerda su aportación y el pub de la esquina lleva el nombre de John Snow.

Más sobre Casarse en Machuria

En un territorio llamado Machuria (no por casualidad, y no situado en un territorio concreto, sino bastante extendido en el tiempo y en el espacio: el machismo), cuando una chica quería casarse tenía que pedir permiso. Iba junto con el chico con el que se había prometido al palacio del ‘jefe’ y este ponía en la mano cerrada de la chica seis trozos de igual longitud de una cuerda fina que sobresalían por los dos lados de su mano; su pretendiente tenía que ir uniéndolos (haciendo nudos) de dos en dos por cada lado de la mano sin que la chica la abriera, para no poder saber los extremos de cada una; cuando estaban hechos los seis nudos la chica abría la mano: si la cuerda salía formando un anillo podían casarse; si no tenían que postergar la boda.

Podían recurrir a una nueva oportunidad igual pasado un año; si esta también era negativa ya no había más oportunidades: no tenían derecho a casarse. ¿Podemos evaluar lo difícil que era casarse en Machuria?

Casarse en Remachuria

Remachuria, territorio cercano a Machuria, tenía un caid todavía más reaccionario que allí, que quería endurecer las condiciones de casamiento respecto a Machuria: aplicaría el mismo procedimiento pero, en vez de con seis, con ocho trozos de cuerda fina.

¿Crees que es más difícil casarse en Remachuria que en Machuria? ¿Cuál es la probabilidad en Remachuria?

SOLUCIONES

Machuria

Parece que el ‘jefe’ del territorio no era muy amigo de los matrimonios entre sus súbditos, porque la probabilidad de que salga un anillo parece ‘evidente’ que es muy pequeña. Pero puede pasar, como muchas otras veces en asuntos relacionados con el azar, que las apariencias engañen.

Vamos a hallar la probabilidad del primer año calculando los casos favorables (CF) y los posibles (CP). Atamos como queramos las cuerdas que salen por uno de los lados de la mano, porque no supone ninguna limitación de lo que sucederá al atar por el otro lado, y es en ese lado donde nos fijamos. Las maneras posibles de atar son las siguientes: en el primer nudo, elegido uno de los extremos lo podremos atar con cualquiera de los otros cinco (5 por tanto); hecho ese primer nudo, elegimos el segundo extremo, para lo que ya solo hay tres para elegir; y atado el segundo nudo ya solo nos quedan dos extremos sueltos y la única posibilidad de elección es atarlos entre sí. Por tanto CP = 5·3·1 = 15.

¿En cuántos de esos casos sale un único anillo? Esos serán los CF. Elegido uno de los extremos, el primer nudo podemos hacerlo con todas las cuerdas excepto con aquella que ya está unida por arriba con ella: cuatro posibilidades; para el segundo nudo tenemos que evitar la cuerda que ya está unida por arriba con ella, dos casos; en el tercero solo quedan dos extremos, luego una sola opción. Con todo eso CF = 4·2·1= 8.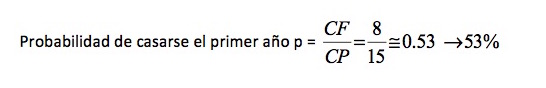                 

Un resultado sorprendente: el primer intento es positivo en más de la mitad de los casos.

Miramos ahora el conjunto de los dos años. La probabilidad de que no salga el anillo en un año es

(1 – p) = 1 – 0.53 = 0.47;

la de que no salga ninguno de los dos años, (que no salga en ninguna de los dos intentos), es el producto de sus probabilidades:

(1-p)·(1-p) = 0.47×0.47 = 0.22

Eso indica que haciendo la prueba dos años seguidos hay una probabilidad del 22% aproximadamente de que no salga un solo anillo ninguno de los dos, que serán las parejas que no se podrán casar. Es decir que podrán casarse, todos los demás: el 78% de los que lo intenten dos años.

La probabilidad de casarse en el segundo año puede verse de otra manera.

La probabilidad de hacer un solo anillo en el segundo intento volverá a ser del 53%, pero considerando solo al 47% que no acertó el primer año, que son los únicos que repetirán la prueba. Como 0.53·0.47 es aproximadamente 0.25, se tiene que el segundo año consigue el anillo el 25% de las parejas que se habían presentado; luego solo hay un 47% – 25% = 22% que no se podrá casar.

Mirándolo de cualquiera de las dos formas, y contra lo que parecía ‘evidente’,

¡no es muy difícil casarse en Machuria!

Puede verse una versión en video del problema ‘Casarse en Machuria’ en este enlace y de su solución aquí.

Remachuria

Por la misma razón que en Machuria, la probabilidad el primer año, será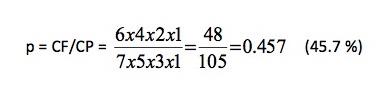En dos años seguidos, la probabilidad de que ninguno salga es

(1-p)·(1-p) = 0.284 (28.4%)

Lo que quiere decir que el 71.6% sí que podían casarse.

¡El caid de Remachuria era bruto pero no muy espabilado con la probabilidad!

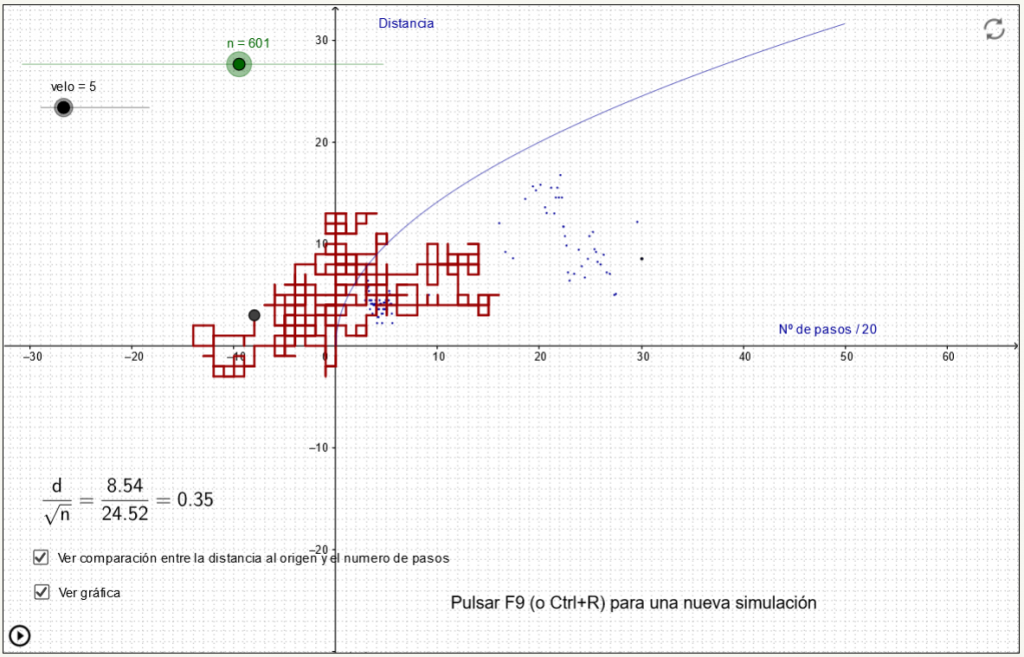
Andar Borracho

El ‘andar del borracho’ es después de dar un paso en una dirección, el paso siguiente puede darlo al azar en cualquier otra dirección (incluido darlo hacia atrás de manera que se vuelva a la situación inicial). Y esa misma elección se repite en cada uno de los pasos que demos.

Viene ahora una pregunta. Si vamos en línea recta y en cada paso avanzamos un metro, al dar N pasos estaremos a N metros del punto de partida. Si hacemos un andar de borracho, ¿cuántos pasos tendremos que dar para avanzar los mismos N metros? O lo que es igual, después de dar N pasos ‘borrachos’, ¿a qué distancia estamos del punto de partida?

[Este problema nos sirve también para hacer modelos de difusión del calor, por ejemplo, porque las moléculas de aire más calientes, las más ‘móviles’, se desplazan de forma aleatoria, como un borracho. Y también puede ser una aproximación a la forma en que se transmiten los patógenos, como pueden ser los virus, en particular los de la COVID 19].

Un modelo simple es tirar un dado para cada movimiento, y en cada uno de los seis resultados tomar la dirección de uno de los vértices de un hexágono para dar el paso siguiente. Se ve así que, en media, para avanzar N metros hacen falta N2 pasos: para alejarnos 10 metros tendremos que dar unos 100 pasos (100 = 102); y la desproporción es mayor cuando mayor es la distancia: para 50 metros ya son 2500 pasos.

¿Se entiende ahora por qué se tarda tanto en calentar una habitación con un radiador? A la dificultad de desplazamiento a distancia además hay que añadir que con la distancia se enfrían las moléculas. Pero a pesar de ello, los virus se propagan a infectan, porque aunque sea difícil, si se está mucho tiempo en una habitación cerrada y sin ventilar acaban llegando a todos los rincones. ¡También del deambular de un borracho podemos sacar conclusiones positivas!

[Para poder experimentar en su formalización en Geogebra con un modelo en que cada paso se puede dar en cuatro direcciones en vez de en seis, se puede consultar aquí]

Preguntas inconvenientes 

La forma habitual de conocer la realidad social es mediante encuestas, pero sobre ellas se suele argumentar que como intervienen personas pueden ocultar información o darla sesgada.

Y sí que lo hacen a veces, sobre todo cuando se quiere obtener información ‘sensible’ o ‘comprometida’, dando respuestas que no se ajustan a la verdad.

Es lo que sucede cuando hacemos preguntas que pueden variar según la población que consideramos, pero que como ejemplo pueden ser:

• • ¿Copias en los exámenes?

• • ¿’Distraes’ algunos productos en los supermercados?

• • ¿Eres homosexual?

• • ¿Has engañado alguna vez a tu pareja?

• • • ¿Ha fumado porros en el último mes?
  • ¿Crees que es conveniente facilitar la entrada de personas del tercer mundo?

• • ¿Piensas que las asignaturas de religión solo se deben impartir en los templos?

Para que una encuesta tenga valor es imprescindible que las respuestas reflejen la verdad, pero no es fácil conseguirlo cuando son cuestiones de carácter íntimo o cuando alguna de las respuestas puede dar una imagen negativa de quien la responda. Si se hacen de forma directa se corre el riesgo de tener un alto porcentaje de no sabe/no contesta y de que las respuestas sean ‘políticamente correctas’, aunque no sean la realidad del entrevistado. Y a pesar de todo se tienen que obtener las respuestas verdaderas.

¿Qué harías para conseguir que la persona a la que se entrevista conteste la verdad manteniendo su privacidad? Busca y discute los procedimientos por los que se podría conseguir.

Respuestas Preguntas comprometidas

El encuestador puede recurrir a las llamadas ‘técnicas de respuesta aleatorizada’, que garantizan la intimidad del entrevistado con lo que se eliminan los motivos para mentir. Puede contestar con sinceridad sin que sea posible saber si ha dicho o no la verdad y, por tanto, cuál ha sido su respuesta, pero, a la vez, permiten averiguar la proporción de respuestas verdaderas que ha habido.

Pongamos un ejemplo concreto de la forma de actuar. La pregunta que hacemos es: ‘¿Intenta defraudar a Hacienda en su Declaración de la Renta?’ (o con más precisión: ‘¿Ha hecho alguna vez trampas en su Declaración de la Renta?’). Preguntando de forma directa puede dar cualquier resultado, porque (casi) nadie va a contestar ‘sí’. Pero se le oferta un modo de operar como el que sigue, que le permite contestar la verdad sin que se pueda saber cuál es en cada caso concreto.

La persona, antes de contestar, tiene que tirar una moneda de forma privada (por ejemplo entrando en una cabina como cuando se va a votar), de forma que nadie verá el resultado. Y se le dice que

• si le sale cara debe responder “sí” (sea cual sea su respuesta verdadera)
• si le sale cruz, responderá la verdad.

Al contestar sí, no se puede saber si es por la moneda o porque de verdad defrauda siempre que puede. El único testigo de lo que le ha salido es el propio encuestado y nadie puede saber la realidad.

¿Qué deducimos del resultado? Tendremos al menos un 50% de respuestas positivas, porque en la moneda sale cara la mitad de las veces. Quien dice que ‘no’ es porque de verdad no defrauda. Pero el resto, las que faltan hasta el 100%, son el porcentaje de defraudadores, que tendremos que multiplicar por dos para tener el porcentaje real. Con unos datos concretos, si hay un 65% de respuestas ‘sí’, quiere decir que del 50% al que le salió cruz en la moneda el 15% dijo que sí, luego que defraudaba de verdad. Como es sobre el 50%, sobre el total es el doble: el porcentaje de defraudadores es del 30%.

Con este procedimiento, si los que contestaron sí es el A% (que tiene que ser mayor que 50), los que realmente defraudan (o cualquier otra pregunta comprometida que se les haga) son 2·(A – 50) %.

El único inconveniente de este método es que se pierden la mitad de las respuestas (aquellas a las que les ha salido cara), por lo que habrá que aumentar el tamaño de la muestra. Si se quiere aprovechar mejor las encuestas, se puede proponer a los encuestados que contesten ‘sí’ (o la respuesta comprometida) tras hacer otro procedimiento aleatorio previo de probabilidad menor de 1/2, por ejemplo 1/3, que se puede conseguir con facilidad con un dado con dos caras pintadas de un color (que será el que hará decir ‘sí’ si nos sale) y las cuatro restantes de otro (que será el que nos hará responder diciendo la verdad).

Si se hiciera así y se obtuviera un porcentaje B de respuestas (ahora B tiene que ser mayor de 1/3 = 33.3%), para calcular el porcentaje real habría que hacer

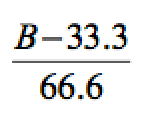
de forma que si B = 50%, el porcentaje real de respuestas ‘sí’ sería , o para B = 70%, .

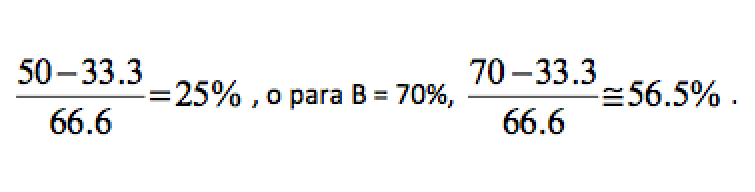
Obviamente se puede utilizar cualquier otro procedimiento para obtener resultados aleatorios, pero es preferible que sean sencillos (del tipo de los propuestos) porque si fueran sofisticados podrían hacer desconfiar a los encuestados y se perdería la utilidad.

Preguntas comprometidas (Respuestas más sofisticadas)

Para que una encuesta tenga valor es imprescindible que las respuestas registradas reflejen la verdad. Conseguirlo no es fácil, sobre todo cuando se trata de cuestiones de carácter íntimo o cuando la pregunta incluye una respuesta que puede promover una imagen negativa de quien la da. Ante este tipo de preguntas es normal que el encuestado se niegue a responder o lo haga mintiendo.

Algunas preguntas comprometidas: ¿Ha hecho alguna vez trampas en su declaración de la renta?; ¿Ha engañado alguna vez a su pareja?; ¿Está afiliado a algún partido político?; ¿Ha estado alguna vez en tratamiento psiquiátrico?; ¿Ha fumado porros en el último mes?

El encuestador puede recurrir a alguna de las técnicas de respuesta aleatorizada, con las que se garantiza la intimidad del entrevistado eliminando los motivos para mentir: puede contestar con sinceridad sin que sea posible saber si ha dicho o no la verdad y, por tanto, cuál ha sido su respuesta. Y a la vez, permiten averiguar la proporción de respuestas verdaderas que ha habido. Se suele decir que estas técnicas permiten saber todo de todos y nada de nadie.

Veamos una técnica de respuesta aleatorizada.

El entrevistador pide al encuestado que utilice un procedimiento aleatorio y, en función del resultado, seleccione la respuesta. Llamamos A y Ā a los resultados considerados en dicho procedimiento, de probabilidades q y 1-q conocidas. (Por ejemplo, elegir una carta de las 10 que se ofrecen, en las que hay 7 oros y 3 copas. Los resultados serían

A: oros y Ā:copas, de probabilidades 0,7 y 0,3).

Si sale A responde con la verdad; si sale Ā  elige la opción más comprometida (“Sí he hecho trampas en la declaración”, “Sí he fumado porros”, …).

Suponiendo que el número de entrevistas es suficientemente grande para que las frecuencias relativas sean aproximadamente iguales a las probabilidades, veamos cómo podemos estimar la proporción p de encuestados que optan sinceramente por la respuesta más comprometida.

Suponemos que se han hecho 1000 entrevistas y se han obtenido 480 respuestas SÍ y 520 NO.

El total de respuestas SI es la suma de las que provienen del suceso A (0,7·1000·p)

y las que provienen del suceso Ā (0,3·1000).  Se cumple así que:

     

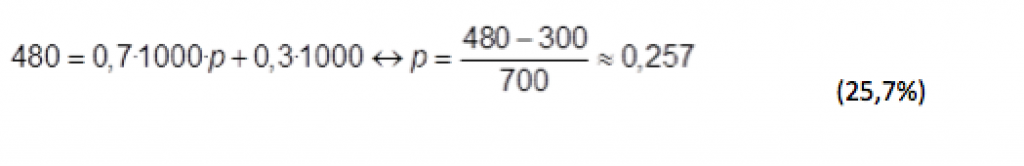
Al mismo resultado llegaríamos dividiendo el número de respuestas SÍ sinceras (480-300) entre el total de respuestas sinceras (700).

En general:

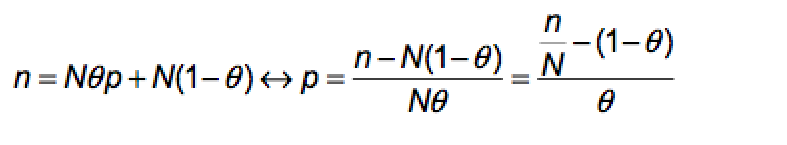
siendo n el número de respuestas SÍ obtenidas, N el número de encuestados y q la probabilidad del resultado A.

[Nota.- Para dar la máxima confianza al encuestado de que su intimidad está a salvo, es recomendable que el valor de q esté comprendido entre 0,5 y 1].

Práctica

Para comprobar la aproximación que se obtiene con estas técnicas haz con tus compañeros una práctica de respuesta aleatorizada.

1. En primer lugar vamos a considerar que la pregunta verdadera es ¿Eres un chico? y que la respuesta comprometida es SÍ. Así sabemos exactamente el verdadero valor de la proporción de respuestas SÍ sinceras.
2. Ahora cada alumno hace esta pregunta a todos los compañeros de clase. La experiencia aleatoria consiste en lanzar dos monedas. Consideraremos como suceso A “salir al menos una cara”, con lo que q = 0,75.
3. Finalmente, se ponen en común todas las encuestas y se calcula la proporción de respuestas SÍ sinceras. El número total de encuestas ha de ser n·(n-1), siendo n el número de alumnos del grupo.